VENN DIAGRAM OF A INTERSECTION B WHOLE COMPLEMENT

Here we are going to see how to draw a venn diagram of A intersection B whole complement.

Venn diagram of (A n B)' : 

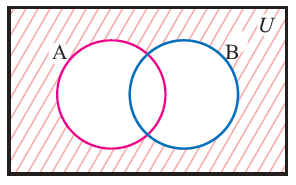
To  represent (A n B)' in venn diagram, we have to shade the region except the common regions of A and B.

(A n B)'

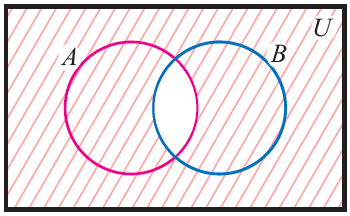
A' U B'

Venn diagrams for (A n B)'  =  A' U B'

Let us look into some examples to understand the above concepts.

Example 1 :

Use the Venn diagram to answer the following questions

List out the elements of the following sets

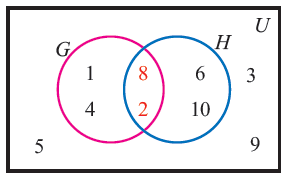
Solution :

(1)  To find the elements of universal set U, we have to list out all the elements that we find in the rectangular box.

U = { 1, 2, 3, 4, 5, 6, 8, 9, 10 }

(2)  To write the elements of set G, we have to list out the numbers that we find in the circle G.

G = { 1, 2, 4, 8}

(3)  To write the elements of set H, we have to list out the numbers that we find in the circle H.

H = { 2, 6, 8, 10}

(4)  To find the elements of the set G', we have to list out all the elements other than the circle G.

G' = { 3, 5, 6, 9, 10 }

(5)  To find the elements of the set H', we have to list out all the elements other than the circle H.

H' = { 1, 3, 4, 5, 9 }

(6) G' n H' = { 3, 5, 9 }

(7) To find (G U H)', first we have to find the elements of

G U H = {1, 2, 4, 6, 8, 10}

(G U H)' = {3, 5, 9}

n (G U H)' = 3

(8) To find (G n H)', first we have to find the elements of 

G n H = { 2, 8}

(G n H)' = { 1, 3, 4, 5, 6, 9, 10 }

n (G n H)' = 7

Example 2 :

If U = {x : 1 ≤ x ≤ 10, x ∊ N}, A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 9, 10}, find

(i) A'    (ii) B'     (iii) A' U B'     (iv) A' ⋂ B'

Solution :

U = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

A = {1, 3, 5, 7, 9}

B = {2, 3, 5, 9, 10}

(i) A' = { 2, 4, 6, 8, 10}

(ii) B' = { 1, 4, 6, 7, 8}

(iii) A' U B' = { 1, 2, 4, 6, 7, 8, 10 }

(iv) A' ⋂ B' = { 4, 6, 8 }

Related topics

• Venn diagram A U B
• Venn diagram A n B
• Venn diagram of A'
• Venn diagram of B'
• Venn diagram of (AUB)'
• Venn diagram of (AnB)'
• Venn diagram of A\B
• Venn diagram of B\A

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.