TESTING CONTINUITY OF A FUNCTION WORKSHEET WITH ANSWERS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
(1) Prove that f(x) = 2x2 + 3x - 5 is continuous at all points in R. Solution
(2) Examine the continuity of the following
(i) x + sin x Solution
(ii) x2 cos x Solution
(iii) ex tan x Solution
(iv) e2x + x2 Solution
(v) x ln x Solution
(vi) sin x / x2 Solution
(vii) (x2 - 16) / (x + 4) Solution
(viii) |x + 2| + |x - 1| Solution
(ix) |x - 2| / |x + 1| Solution
(x) cot x + tan x Solution
(3) Find the points of discontinuity of the function f, where
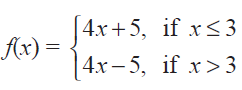
(ii)
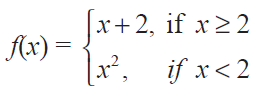
(iii)
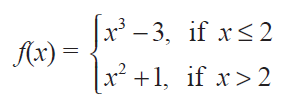
(iv)
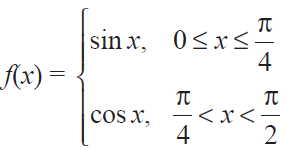
(4) At the given point x0 discover whether the given function is continuous or discontinuous citing the reasons for your answer :
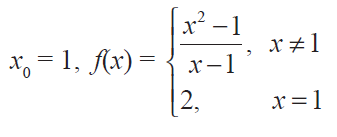
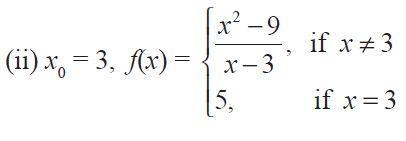
(5) Show that the function
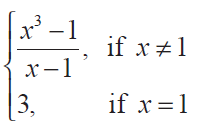
is continuous on (- ∞, ∞). Solution
(6) For what value of a is this function f(x) =
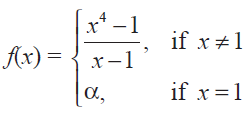
continuous at x = 1 ? Solution
(7) Let f(x)
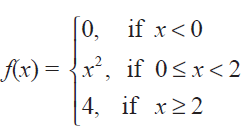
Graph the function. Show that f(x) continuous on (- ∞, ∞).
(8) If f and g are continuous functions with f(3) = 5 and lim x->3 [2 f(x) - g(x)] = 4, find g(3). Solution
(9) Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
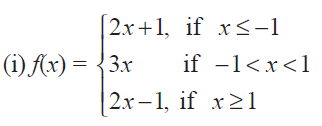
(10) A function f is defined as follows :
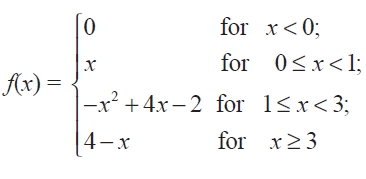
Is the function continuous?
(11) Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
(i) f(x) = (x2 - 2x - 8)/(x + 2), x0 = -2 Solution
(ii) f(x) = (x3 + 64)/(x + 4), x0 = -4 Solution
(iii) f(x) = (3 - √x)/(9 - x), x0 = 9 Solution
(12) Find the constant b that makes g continuous on (−∞, ∞)
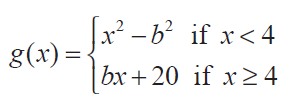
(13) Consider the function f (x) = x sin π/x What value must we give f(0) in order to make the function continuous everywhere? Solution
(14) The function f(x) = (x2 - 1) / (x3 - 1) is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x = 1 ? Solution
(15) State how continuity is destroyed at x = x0 for each of the following graphs.
(i)
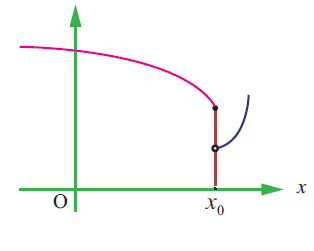
(ii)
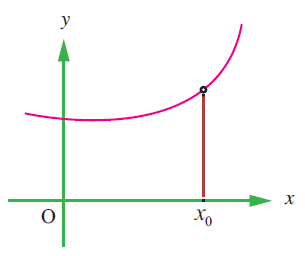
(iii)
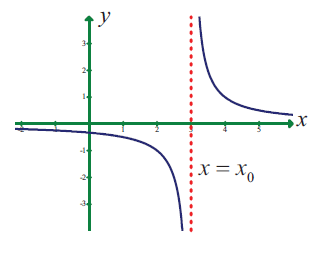
(iv)
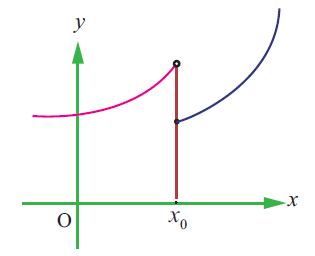
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
