HOW TO FIND POINTS OF DISCONTINUITY FOR A PIECEWISE FUNCTION

Example 1 :

Find the points of discontinuity of the function f, where

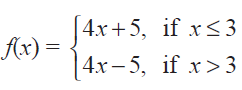
Solution :

For the values of x greater than 3, we have to select the function 4x + 5.

lim _x->3- f(x)  =  lim _x->3- 4x + 5

  =  4(3) + 5 

  =  12 + 5

  =  17  -------(1)

For the values of x lesser than 3, we have to select the function 4x - 5.

lim _x->3+ f(x)  =  lim _x->3+ 4x - 5

  =  4(3) - 5 

  =  12 - 5

  =  7  -------(2)

lim _x->3- f(x) ≠ lim _x->3+ f(x)

So, the given piece-wise function is not continuous at

x  =  3

Example 2 :

Find the points of discontinuity of the function f, where

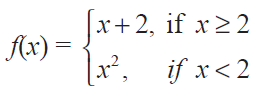
Solution :

For the values of x greater than 2, we have to select the function x + 2.

lim _x->2- f(x)  =  lim _x->2- x + 2

  =  2 + 2

       =  4  -------(1)

For the values of x lesser than 2, we have to select the function x².

lim _x->2+ f(x)  =  lim _x->2+ x²

  =  2²

       =  4-------(2)

lim _x->2- f(x) =  lim _x->2+ f(x)

The function is continuous at x = 2.

So, the given piece-wise function is continuous for all real values of x. 

That is, 

x ∈ R

Example 3 :

Find the points of discontinuity of the function f, where

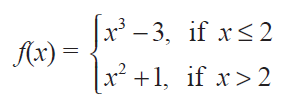
Solution :

For the values of x greater than 2, we have to select the function x² + 1

lim _x->2- f(x)  =  lim _x->2- x² + 1

  =   2² + 1

       =  5  -------(1)

For the values of x lesser than 2, we have to select the function x³ - 3.

lim _x->2+ f(x)  =  lim _x->2+ x³ - 3

  =  2³ - 3

=  8 - 3

       =  5-------(2)

lim _x->2- f(x) =  lim _x->2+ f(x)

The function is continuous at x  =  2.

So, the given piece-wise function is continuous for all real values of x. 

That is,

x ∈ R

Example 4 :

Find the points of discontinuity of the function f, where

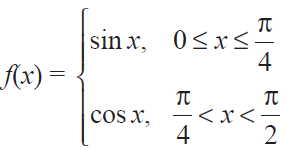
Solution :

Here we are going to check the continuity between 0 and π/2.

For the values of x lesser than or equal to π/4, we have to choose the function sin x.

lim _x->π/4- f(x)  =  lim _x->π/4^- sin x

       =  sin (π/4)

=  1/√2

For the values of x greater than π/4, we have to choose the function cos x .

lim _x->π/4+ f(x)  =  lim _x->π/4⁺ cos x

       =  cos (π/4)

=  1/√2

The function is continuous for all x ∈ [0, π/2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.