HOW TO DETERMINE IF A FUNCTION IS CONTINUOUS ON A GRAPH

Question 1 :

State how continuity is destroyed at x = x₀ for each of the following graphs.

(i)  

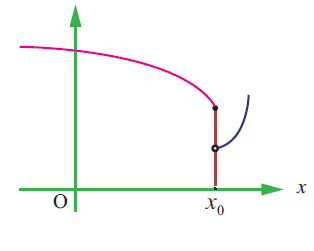
Solution :

By observing the given graph, we come to know that 

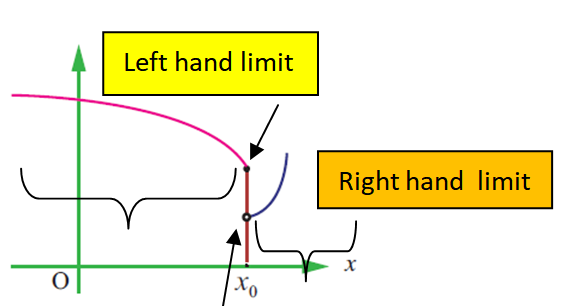
lim _{x-> x0-} f(x)  =  f(x₀)  (Because we have filled circle)

But,

lim _{x-> x0+} f(x)  ≠  f(x₀)  (Because we have unfilled circle)

Hence the given function is not continuous at the point x = x₀.

(ii)  

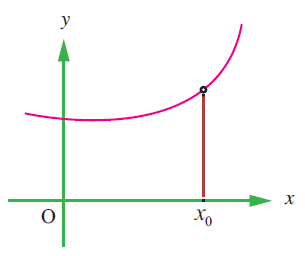
Solution :

By observing the given graph, we come to know that 

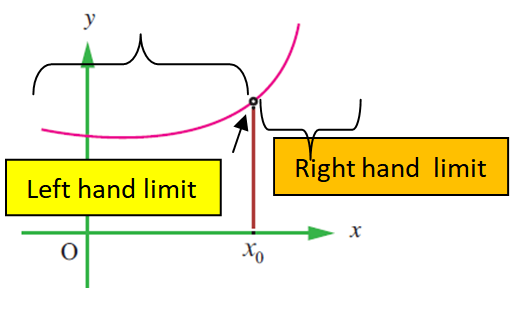
lim _{x-> x0-} f(x)  =  f(x₀)  (Because we have unfilled circle)

But,

lim _{x-> x0+} f(x)  =  f(x₀)  (Because we have the same unfilled circle at the same place)

Hence the given function is continuous at the point x = x₀.

(iii)

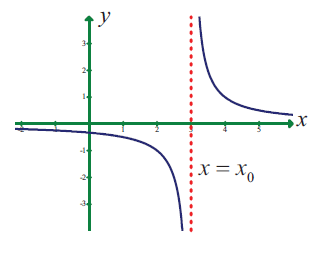
Solution :

From the given picture, we know that lim _{x-> x0-} f(x)  =  -∞

But,

lim _{x-> x0-} f(x)  = -∞

Hence it is not continuous at x = x_0.

(iv)

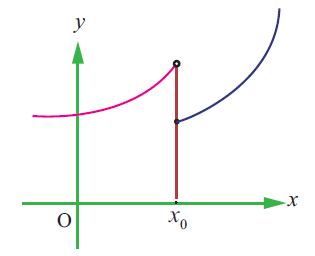
Solution :

lim _{x-> x0-} f(x)  =  f(x₀)  (Because we have unfilled circle)

But,

lim _{x-> x0+} f(x)  ≠  f(x₀)  (Because we have filled circle at different place)

Hence the given function is not continuous at the point x = x₀.

Question 2 :

Consider the function f (x) = x sin π/x What value must we give f(0) in order to make the function continuous everywhere?

Solution :

f (x) = x sin π/x 

Range of sin x is [-1, 1]

-1  ≤ sin π/x  ≤ 1

By multiplying x throught the equation, we get

-x  ≤ x (sin π/x)  ≤ x

Now let us apply the limit values

lim _{x -> 0} (-x)  ≤ lim _{x -> 0} x (sin π/x)  ≤ lim _{x -> 0} x

0 ≤ lim _{x -> 0} x (sin π/x)  ≤ 0

By sandwich theorem 

lim _{x -> 0} x (sin π/x)  =  0

Now let us redefine the function

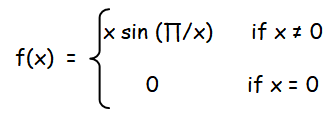
From this we come to know the value of f(0) must be 0,  in order to make the function continuous everywhere

Question 3 :

The function f(x)  =  (x² - 1) / (x³ - 1) is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x = 1 ?

Solution :

By applying the limit value directly in the function, we get 0/0.

Now let us simplify f(x)

f(x)  =  (x² - 1) / (x³ - 1)

  =  (x + 1) (x - 1)/(x - 1)(x² + x + 1)

  =  (x + 1) / (x² + x + 1)

lim _{x-> 1} f(x)   = lim _{x-> 1}  (x + 1) / (x² + x + 1)

  =  (1 + 1)/ (1 + 1 + 1)

  =  2/3

By redefining the function, we get

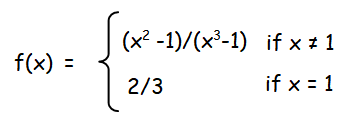
From this we come to know the value of f(1) must be 2/3,  in order to make the function continuous everywhere

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.