HOW TO CHECK THE CONTINUITY OF A FUNCTION AT A POINT

In order to check if the given function is continuous at the given point x = x₀, it has to satisfy the conditions given below.

(i)  lim x -> x₀⁺  f(x) exists

(ii)  lim x -> x₀-  f(x) exists

(iii)  lim x-> x₀+ f(x)  =  lim x -> x₀-  =  L

Question 1 :

At the given point x₀ discover whether the given function is continuous or discontinuous citing the reasons for your answer :

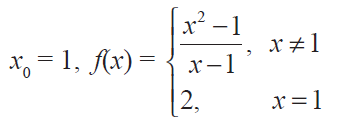
Solution :

f(x)  =  (x² - 1)/(x - 1)

  =  (x - 1) (x + 1)/(x - 1)

f(x)  =  (x + 1)

lim x->1^- f(x)  =  1 + 1  =  2     ------(1)

lim x->1⁺ f(x)  =  1 + 1  =  2    ------(2)

f(1)  =  2    ------(3)

lim x->1^- f(x)  =  lim x->1⁺ f(x)  =  f (1)

Hence the function is continuous at the point x₀ = 1.

Question 2 :

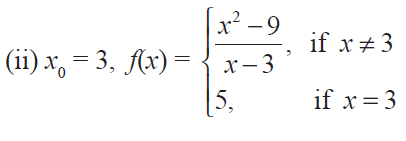
Solution :

f(x)  =  (x² - 9)/(x - 3)

  =  (x - 3) (x + 3)/(x - 3)

f(x)  =  (x + 3)

lim x->3^- f(x)  =  3 + 3  =  6     ------(1)

lim x->3⁺ f(x)  =  3 + 3  =  6    ------(2)

f(3)  =  5    ------(3)

lim x->3^- f(x)  =  lim x->3⁺ f(x)  ≠  f (3)

Hence the function is not continuous at the point x₀ = 3.

Question 3 :

Show that the function

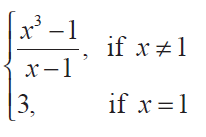
is continuous on (- ∞, ∞).

Solution :

f(x)  =  (x³ - 1)/(x - 1)

  =  (x - 1) (x² + x + 1)/(x - 1)

f(x)  =  (x² + x + 1)

lim x->1^- f(x)  =  1² + 1 + 1

  =  3     ------(1)

lim x->1⁺ f(x)  =  1² + 1 + 1

  =  3     ------(2)

f(1)  =  3    ------(3)

lim x->1^- f(x)  =  lim x->1⁺ f(x)  =  f (1)

Hence the function is not continuous at the point x₀ = 1.

Question 4 :

For what value of a is this function f(x) = 

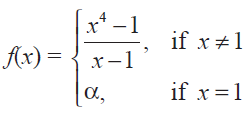
continuous at x = 1 ?

Solution :

If the given function is continuous at a point x->a, then 

lim _x->a- f(x)  =  lim _x->a+ f(x)  =  lim _x->af(x)

f(x)  =  (x⁴ - 1) / (x - 1)

 =  ((x²)² - 1) / (x - 1)

 =  (x²+ 1)(x² - 1) / (x - 1)

 =  (x²+ 1)(x + 1)(x - 1) / (x - 1)

f(x)  =  (x² + 1)(x + 1)

lim _x->1-  f(x)  =  (1² + 1)(1 + 1)  =  4  ---(1)

lim _x->1+  f(x)  =  (1² + 1)(1 + 1)  =  4 ---(2)

lim _x->1 f(x)  = a ---(3)

(1)  =  (2)  =  (3)

4 = 4 = a

Hence the value of a is 4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.