SKETCH THE GRAPH AND VERIFY THE CONTINUITY OF THE FUNCTION
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Let f(x)
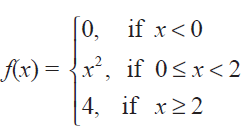
Graph the function. Show that f(x) continuous on (- ∞, ∞).
Solution :
There are three partitions in the piecewise function.
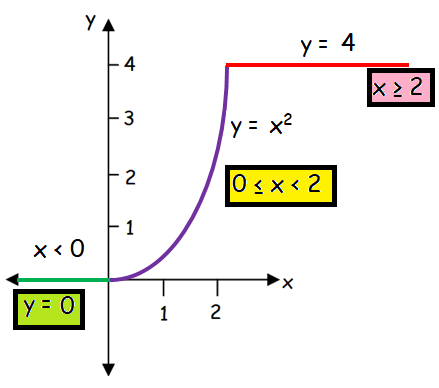
To check the continuity at the point 0, we should prove the following.
lim x-> 0- f(x) = lim x->0+ f(x) = lim x->0 f(0)
lim x-> 0- f(x) = 0 ----(1)
lim x->0+ f(x) = 0 ----(2)
f(0) = 0 ----(3)
(1) = (2) = (3)
Hence the function is continuous at x = 0.
Now let us check the continuity at the point 2.
lim x-> 2- f(x) = lim x->2+ f(x) = lim x->2 f(0)
lim x-> 2- f(x) = 22 = 4 ----(1)
lim x->2+ f(x) = 4 ----(2)
f(2) = 4 ----(3)
(1) = (2) = (3)
Hence the function is continuous at x = 2.
So the given piecewise function is continuous on (- ∞, ∞).
Question 2 :
If f and g are continuous functions with f(3) = 5 and lim x->3 [2 f(x) - g(x)] = 4, find g(3).
Solution :
lim x->3 [2 f(x) - g(x)] = 4
Let us apply 3 in the function instead of x.
[2 f(3) - g(3)] = 4
2(5) - g(3) = 4
10 - g(3) = 4
g(3) = 10 - 4
g(3) = 6
Hence the value of g(3) is 6.
Question 3 :
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
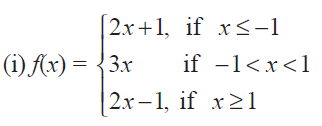
Solution :
First let us check the continuity at the point x = -1
lim x-> -1- f(x) = lim x-> -1- 2x + 1
By applying the limit, we get
= 2(-1) + 1
= -2 + 1
= -1 -----(1)
lim x-> -1+ f(x) = lim x-> -1+ 3x
By applying the limit, we get
= 3(-1)
= -3 -----(2)
lim x-> -1- f(x) ≠ lim x-> -1+
So, the function is not continuous at x = -1.
Now let us check the continuity at the point x = 1
lim x-> 1- f(x) = lim x-> 1- 3x
By applying the limit, we get
= 3(1)
= 3 -----(1)
lim x-> -1+ f(x) = lim x-> -1+ 2x - 1
By applying the limit, we get
= 2(1) - 1
= 1 -----(2)
lim x-> 1- f(x) ≠ lim x-> 1+
So, the function is not continuous at x = 1.
To find at which of these points f is continuous from the right, from the left, or neither, we have to draw the number line.
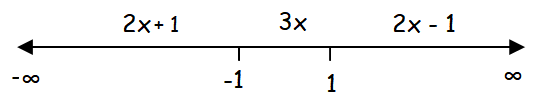
let x0 ∈ (-∞, -1]
lim x-> x0 f(x) = lim x-> x0 2x + 1
Applying the limit, we get
= 2x0 + 1 ------(1)
f(x0) = 2x0 + 1 ------(2)
(1) = (2)
It is continuous in (-∞, -1].
let x0 ∈ (-1, -1)
lim x-> x0 f(x) = lim x-> x0 3x
Applying the limit, we get
= 3x0 ------(1)
f(x0) = 3x0 ------(2)
(1) = (2)
It is continuous in (-1, 1).
let x0 ∈ [1, ∞)
lim x-> x0 f(x) = lim x-> x0 2x - 1
Applying the limit, we get
= 2x0 - 1 ------(1)
f(x0) = 2x0 - 1 ------(2)
(1) = (2)
It is continuous in [1, ∞).
Graph of f(x) = 2x + 1 :
|
x = -1 f(-1) = -1 |
x = -2 f(-2) = -3 |
x = -3 f(-3) = -5 |
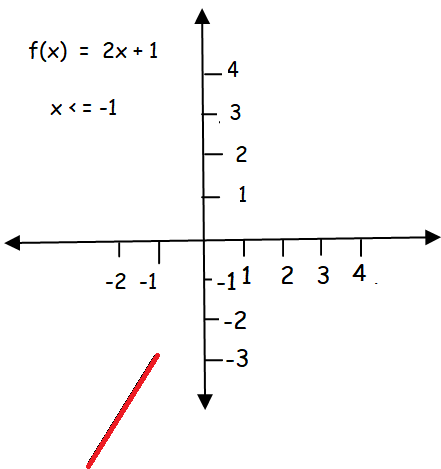
Graph of f(x) = 3x :
-1 < x < 1
|
x = -0.5 f(-0.5) = -1.5 |
x = -0.7 f(-0.7) = -2.1 |
x = 0.5 f(0.5) = 1.5 |
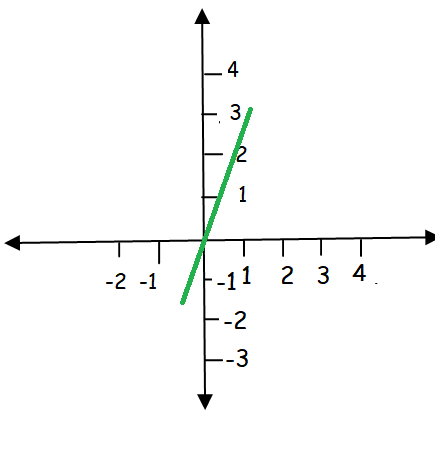
Graph of f(x) = 2x - 1:
x > = 1
|
x = 1 f(1) = 1 |
x = 2 f(2) = 3 |
x = 3 f(3) = 5 |
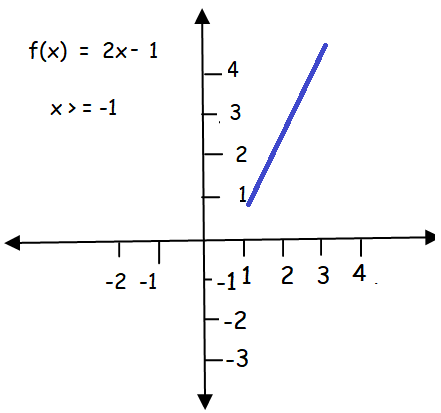
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
