HOW TO CHECK CONTINUITY OF MODULUS FUNCTION

How to Check Continuity of Modulus Function :

Here we are going to how to examine the continuity of the modulus function.

To know the points to be remembered in order to decide whether the function is continuous at particular point or not, you may look into the page " How to Check Continuity of a Function If Interval is not Given "

Question 1 :

Examine the continuity of the following 

|x + 2| + |x - 1|

Solution :

Since we have a absolute value function, we have to split into piece wise function and check its continuity.

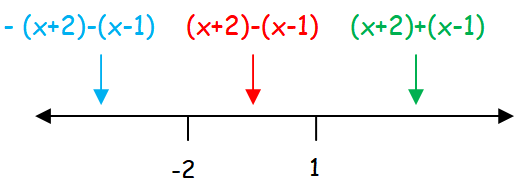
f(x)  =  -x - 2 - x + 1  =  -2x - 1     If x < -2

f(x)  =  x + 2 - x + 1  =  3      If -2 ≤ x < 1

f(x)  =  x + 2 + x - 1  =  2x + 1   If x ≥ 1

From the above piece wise function, we have to check if it is continuous at x = -2 and x = 1

Since left hand limit and right hand limit are equal for -2, it is continuous at x = -2.

Since left hand limit and right hand limit are equal for 1, it is continuous at x = 1.

Hence the function is continuous for all x ∈ R.

Question 2 :

Examine the continuity of the following 

|x - 2| / |x + 1|

Solution :

x - 2  =  0          x + 1  =  0

x  =  2    x  =  -1

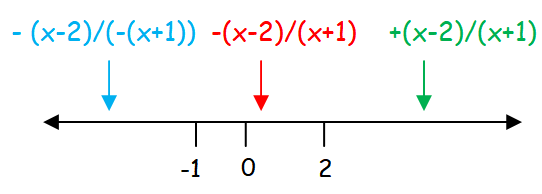
f(x)  =  (x-2)/(x+1)     If x < -1

f(x)  =  -[(x-2)/(x+1)]     If -1 < x < 2

f(x)  =  (x-2)/(x+1)      If x > 2

From the above piece wise function, we have to check if it is continuous at x = -1 and x = 2

lim x_->-1- f(x)

   =  (-1-2)/(-1+1)

  =  -3/0

  =  - ∞

The function is not continuous at x = -1.

Now we need to check if it is continuous at x = 2

It is continuous at x = 2.

Hence the function is continuous for  all x ∈ R - {-1}.

Question 3 :

Examine the continuity of the following 

cot x + tan x

Solution :

Let f(x)  =  cot x + tan x

The function is continuous except sin 2x = 0

sin 2x = sin 0

2x = n π + (-1)ⁿ α

2x = n π + (-1)ⁿ 0

2x = n π

x = (n/2)π

So, the function is continuous for all real values except 

x = (n/2)π

After having gone through the stuff given above, we hope that the students would have understood, "How to Check Continuity of Modulus Function"

Apart from the stuff given in "How to Check Continuity of Modulus Function",  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.