PSAT MATH QUESTIONS AND ANSWERS

Question 1 :

Convert 7/20 to decimal form.

Solution :

In order to find the decimal form of the given fraction, we have to convert the denominator as 10, 100, 1000, etc.

Now we have 20 in the denominator, in order to convert it as 100, we have to multiply both numerator and denominator by 5.

So, we get

  =  (7/20) ⋅ (5/5)

  =  35/100

  =  0.35

Hence the decimal form of 7/20 is 0.35.

Question 2 :

Find the value of 500, 000 + 400 + 5.

Solution :

By adding 400 and 5, we get 405. So we have to change the last three digits of 500, 000.

So, we get 500405.

Question 3 :

If x = 4 and y = 3, what is (x + y)² ?

Solution :

In order to find the value of (x + y)², first we have to find the value of x + y.

x + y  =  4 + 3  = 7

(x + y)²  =  7²  =  49

Question 4 :

(√144)(√16) 

Solution :

√144  =  √(12 ⋅ 12)  =  12

√16  =  √(4 ⋅ 4)  =  4

(√144) (√16)  =  12 ⋅ 4  =   48

Hence the answer is 48.

Question 5 :

1 knot  =  3 vines

2 shings  =  4 knots

How many Shings are in 9 Vines ?

Solution :

Given that :

1 knot  =  3 vines  ---(1)

4 knots  =  2 shings

1 knot  =  (1/2) shings  ----(2)

(1)  =  (2) 

3 vines  =  (1/2) shings

By multiplying 3 on both sides, we get

9 vines  =  (3/2) shings

Hence the answer is 3/2 shings.

Question 6 :

What numbers is half way between 2 ⋅ (3/6) and 4?

Solution :

First let us simplify

2 ⋅ (3/6) =  1

The number between 1 and 4 are 2 and 3.

To find the half way, we have to find the average of 2 and 3.

  =  (2 + 3)/2  =  2.5

Hence the answer is 2.5.

Question 7 :

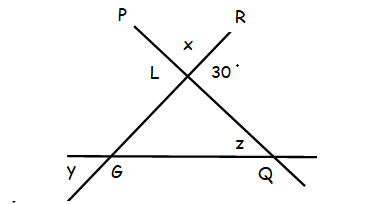
In the figure given below LGQ is a triangle. What is z in terms of y?

Solution :

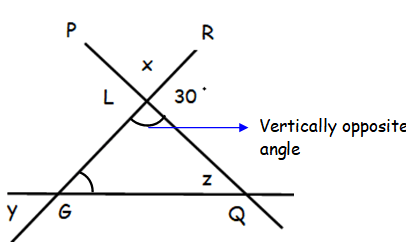
∠PLR + ∠RLQ = 180°

x + 30° = 180°

x  =  180° - 30° = 150°

∠RGQ = y.

x + y + z = 180°

150° + y + z = 180°

z = 180° - 150° - y

z = 30° - y

Hence, the required angle is 30° - y.

Question 8 :

-2 + 5(-18 ÷ 3 + 9) - 13  

Solution :

By using  PEMDAS rule, first we have to simplify the terms inside the parenthesis.

  = -2 + 5(-18 ÷ 3 + 9) - 13 

In the parenthesis, we have to perform division.

  = -2 + 5(-6 + 9) - 13

  = -2 + 5(3) - 13

Then we have to perform multiplication.

  = -2 + 15 - 13

  = -15 + 15

  = 0

Question 9 :

The are of a square is equal to the area of circle, whose diameter is 10. What is the length of a side of the square ?

Solution :

Area of square = Area of circle

a² = π r²

Diameter of the circle = 10 

Radius of circle = 10/2 = 5

a² = π (5)²

a² = 25 π 

a = √(25π)

a = 5√π

Hence the side length of square is 5√π.

Question 10 :

4a(3b - 6)

Solution :

We have to distribute 4a with the terms inside the parenthesis.

= 4a(3b - 6)

= 12ab - 24a

PSAT Math Worksheets

PSAT practice test math - 1

PSAT practice test math - 2

PSAT practice test math - 3

PSAT practice test math - 4

PSAT practice test math - 5

PSAT practice test math - 6

PSAT practice test math - 7

PSAT practice test math - 8

PSAT practice test math - 9

PSAT practice test math - 10

PSAT practice test math - 11

Hardest PSAT Math Questions with Answers

Part - 1

Part - 2

Part - 3

Study Material for SAT Math

SAT Math Practice

SAT Math Worksheets

Hardest SAT Math Questions with Answers

Part - 1

Part - 2

Part - 3

Part - 4

Part - 5

Part - 6

Part - 7

Part  - 8

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.