HARDEST PSAT MATH QUESTIONS (Part - 2)

Question 1 :

In a college archeology class, 78 students are going to a dig site to find and study artifacts. The dig site has been divided into 24 sections, and each section will be studied by a group of either 2 or 4 students. How many of the sections will be studied by a group of 2 students?

Answer :

Let x be the number of groups with 2 students y be the number of groups with 4 students. 

Then, 

2x + 4y  =  78 ----> x + 2y  =  39 ----(1)

x + y  =  24 ----(2)

(1) - (2) : 

y  =  15

Substitute 17 for y in (2). 

x + 15  =  24

x  =  9

So, 9 sections will be studied by a group of 2 students. 

Question 2 :

If f(x - 1) = 2x + 3 for all values of x, what is the value of f(-3)?

(A) -7           (B) -5           (C) -3           (D) -1

Answer :

f(x - 1)  =  2x + 3 ----(1)

Let y = x - 1 ---> x = y + 1. 

f(y)  =  2(y + 1) + 3

f(y)  =  2y + 2 + 3

f(y)  =  2y + 5

Substitute -3 for y. 

f(-3)  =  2(-3) + 5

f(-3)  =  -6 + 5

f(-3)  =  -1

The correct answer is (D).

Question 3 :

(x²y³)^1/2(x²y³)^1/3  =  x^a/3y^a/2

If the equation above, where a is a constant, is true for all positive values of x and y, what is the value of a?

(A) 2           (B) 3           (C) 5           (D) 6

Answer :

(x²y³)^1/2(x²y³)^1/3  =  x^a/3y^a/2

(x²y³)^{1/2 + 1/3}  =  x^a/3y^a/2

(x²y³)^{(3 + 2)/6}  =  x^a/3y^a/2

(x²y³)^5/6  =  x^a/3y^a/2

(x²)^5/6(y³)^5/6  =  x^a/3y^a/2

x^5/3y^5/2  =  x^a/3y^a/2

x^5/3y^5/2  =  x^a/3y^a/2

Since the equation is true for all positive values of x and y, it follows that the corresponding exponents of x and y on both sides of the equation must be equal. 

a/3  =  5/3

a  =  5

The correct answer is (C).

Question 4 :

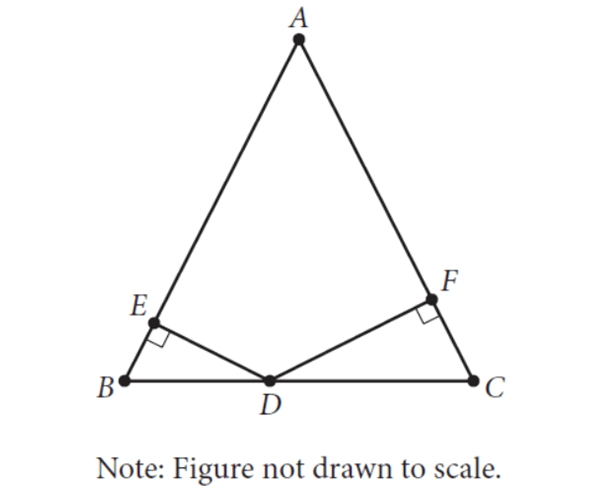
Triangle ABC above is isosceles with AB = AC and BC = 48. The ratio of DE to DF is 5 : 7. What is the length of DC?

(A) 12           (B) 20           (C) 24           (D) 28

Answer :

m∠E  =  m∠F  =  90°

Since triangle ABC above is isosceles with AB = AC,

m∠B  =  m∠C

By Angle-Angle (AA) similarity postulate, triangles BED and CFD are similar.

DB/DC  =  DE/DF

Given : DE/DF  =  5/7.

DB/DC  =  5/7

DC/DB  =  7/5

5(DC)  =  7(DB) ----(1)

Given : BC = 48. 

BC  =  48

DB + DC  =  48

DB  =  48 - DC

Substitute (48 - DC) for DB in (1).

5(DC)  =  7(48 - DC)

5(DC)  =  336 - 7(DC)

12(DC)  =  336

DC  =  28

The correct answer is (D).

Question 5 :

If x - 2 is a factor of x² - bx + b where b is a constant, what is the value of b?

Answer :

Let P(x) = x² - bx + b. 

Since (x - 2) is a factor of P(x), by Factor Theorem, 

P(2)  =  0

2² - b(2) + b  =  0

4 - 2b + b  =  0

4 - b  =  0

b  =  4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.