HARDEST PSAT MATH QUESTIONS (Part - 1)

Question 1 :

Boyd grows only tomatoes and raspberries in his garden. Last year, he grew 140 pounds of tomatoes and 60 pounds of raspberries. This year, the production, by weight, of tomatoes declined by 20 percent, and the production, by weight, of raspberries declined by 50 percent. By what percentage did the total yield, by weight, of Boyd’s garden decline?

A. 29 percent  B. 30 percent  C. 35 percent  D. 70 percent

Answer :

Production of tomatoes last year = 140 lb.

Production of raspberries last year = 60 lb.

Total yield (last year) :

= 140 + 60

= 200 lb

Production of tomatoes this year :

= 0.8 ⋅ 140

= 112 lb

Production of raspberries this year :

= 0.5 ⋅ 60

= 30 lb

Total yield (this year) :

= 112 + 30

= 142 lb

Total yield declined by weight :

= 200 - 142

= 58 lb

By percentage the total yield, by weight, of Boyd’s garden declined :

= (58/200) ⋅ 100%

= 29%

The correct answer is (A).

Question 2 :

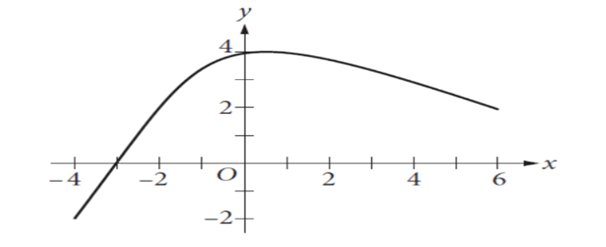
What is the minimum value of the function graphed on the xy-plane above, for -4 ≤ x ≤ 6?

(A) -∞           (B) -4           (C) -2           (D) 1

Answer :

The question targets the minimum value of the function,  for -4 ≤ x ≤ 6. In the above graph, minimum value of the function occurs at the point (-4, -2) for -4 ≤ x ≤ 6. So, the minimum value is -2.

The correct answer is (C).

Question 3 :

A high school developed a program called Propel, which  offers extra guidance and support during the 9th-grade year. Before the school year began, 327 rising 9th graders were selected at random to participate in a study; 109 of those students were randomly assigned to enroll in the Propel program and the remaining students served as a control group. A summary of the year-end grade point averages (GPA) for the 327 9th-grade students who were chosen for the study is shown in the table below.

Of the students enrolled in the Propel program, the ratio of boys to girls is approximately 2:3. Which of the following is the best estimate of the number of girls enrolled in the program?

(A) 44           (B) 65           (C) 73           (D) 131

Answer :

Total number of students enrolled in Propel :

= 61 + 48

= 109

Given : Of the students enrolled in the Propel program, the ratio of boys to girls is approximately 2 : 3.

no. of boys enrolled in Propel : 2x

no. of girls enrolled in Propel : 3x

Total number of students enrolled in Propel :

= 2x + 3x

= 5x

Then,

5x = 109

x = 21.8

Number of girls enrolled in Propel :

= 3 ⋅ 21.8

= 65.4

≈ 65

The correct answer is (B).

Question 4 :

An artist is creating a sculpture using bendable metal rods of equal length. One rod is formed into the shape of a square and another rod into the shape of an equilateral triangle. If each side of the triangle is 2 inches longer than each side of the square, how long, in inches, is each rod?

(A) 16           (B) 18           (C) 24           (D) 30

Answer :

Let x be the length of each side of the square.

Then, the length of each side of the triangle is (x + 2).

Perimeter of the square  =  4x.

Perimeter of the triangle  =  3(x + 2).

Since the metal rods are of equal length,

4x = 3(x + 2)

4x = 3x + 6

x = 6

To know the length of each rod, substitute 6 for x either in the perimeter of square or triangle.

= 4 ⋅ 6

= 24 inches

The correct answer is (C).

Question 5 :

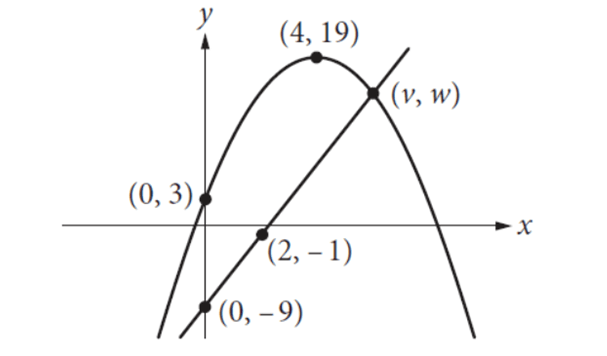
The xy-plane above shows one of the two points of intersection of the graphs of a linear function and a quadratic function. The shown point of intersection has coordinates (v, w). If the vertex of the graph of the quadratic function is at (4, 19), what is the value of v?

Answer :

Find the equation of the parabola :

Vertex form equation of a parabola :

y  =  a(x - h)² + k

Vertex (h, k)  =  (4, 19).

y  =  a(x - 4)² + 19

In the above graph, the parabola is passing through the point (0, 3). Then,

3 = a(0 - 4)² + 19

3 = 16a + 19

-16 = 16a

-1 = a

Equation of the parabola :

y = -1(x - 4)² + 19

y = -(x - 4)² + 19 ----(1)

Find the equation of the line :

The line is passing through the point (0, -9) and (2, -1).

Slope of the line :

m = (y₂ - y₁)/(x₂ - x₁)

Substitute (x₁, y₁) = (0, -9) and (x₂, y₂) = (2, -1).

m = (-1 + 9)/(2 - 0)

m = 8/2

m = 4

y-intercept of the line is (0, -9).

Equation of the line in slope-intercept form :

y = mx + b

Slope m = 4 and y-intercept b = -9.

y = 4x - 9 ----(2)

Solve (1) and (2) to get the x-coordinate at the point of intersection of the parabola and line.

(1) = (2)

y = y

-(x - 4)² + 19 = 4x - 9

-(x² - 8x + 16) + 19 = 4x - 9

-x² + 8x - 16 + 19 = 4x - 9

-x² + 8x + 3 = 4x - 9

-x² + 4x + 12 = 0

x² - 4x - 12 = 0

(x - 6)(x + 2) = 0

(v, w) is the point of intersection of the parabola and line. As (v, w) is on the positive side of x-axis, v (x-coordinate) has to be positive.

So, v = 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.