WORKSHEET FOR OPERATIONS ON COMPLEX NUMBERS IN POLAR FORM

Find the product of complex numbers in polar form

1) 

z1  =  7(cos 25˚ + i sin 25˚)

z2  =  2(cos 130˚ + i sin 130˚)

Solution

2)  

z1  =  √2(cos 118˚ + i sin 118˚)

z2  =  0.5(cos (-19˚) + i sin (-19˚)

Solution

3)

z1  =  5(cos π/4 + i sin π/4)

z2  =  3(cos 5π/4 + i sin 5π/4)

Solution

4)  

z1  =  √3(cos 3π/4 + i sin 3π/4)

z2  =  1/3(cos π/6 + i sin π/6)

Solution

Write your answer in rectangular form when rectangular form is given and in polar form when polar form is given.

5)  (4 + 4i) (5 - 3i)        Solution

6)  4√2(cos 7π/4 + i sin 7π/4) ⋅ 2(cos π/6 + i sin π/6)

Solution

7)  [2√2(cos 7π/6 + i sin 7π/6)] / [6(cos 11π/6 + i sin 11π/6)]

Solution

Find the product of the complex numbers in polar form. Answer in both polar form and rectangular form.

8)  𝑧1 = 4(cos 225° + 𝑖sin 225°) and 𝑧2 = 3(cos 90° + 𝑖sin 90°)

Solution

9)  𝑧1 = √2(cos 2π/3 + 𝑖 sin 2π/3) and 𝑧2 = 1/5(cos π/6 + 𝑖sin π/6)

Solution

Find the quotient of the complex numbers in polar form: 𝑧1/𝑧2 Write the answer in both polar form and rectangular form. 

10)  𝑧1 = 2(cos 210° + 𝑖sin 210°) and 𝑧2 = 8(cos 60° + 𝑖sin 60°)

Solution

11)  𝑧1 = 2/5 (cos𝜋/2 +𝑖 sin 𝜋/2) and 𝑧2 = 1/2 (cos 5𝜋/4 + 𝑖 sin 5𝜋/4)

Solution

Answers :

1)  14(cis (155˚))

2)  (1/√2)(cis (99˚))

3)   15(cis (23π/12))

4)  (1/√3)(cis (11π/12))

Find the quotient of complex numbers in polar form

1)  z1  =  2(cis (30˚)) and z2  =  3(cis (60˚))

2)  z1  =  5(cis (220˚)) and z2  =  2(cis (115˚))

3)  z1  =  6(cis (5π)) and z2  =  3(cis (2π))

4)  z1  =  cis (π/2) and z2  =  cis (π/4)

Solution

Answers :

1)  (2/3)(cis (-30˚))

2)   5/2(cis (105˚))

3)  2(cis (3π))

4)  cis (π/4)

(1)  Write in polar form of the following complex numbers

(i) 2 + i 2√3

(ii) 3 - i √3(iii) −2 − i2

(iv) (i - 1) / [cos (π/3) + i sin  (π/3)]       Solution

(2)  Find the rectangular form of the complex numbers

(i) [cos (π/6) + i sin (π/6)] [cos (π/12) + i sin (π/12)] 

(ii) [cos (π/6) - i sin (π/6)]/2 [cos (π/3) + i sin (π/3)]  

Solution

(3)  If (x1 + iy1) (x2 + iy2) (x3 + iy3) ................(xn + iyn)  =  a + ib show that 

(i)  (x12 + y12) (x22 + y22)............ (xn2 + yn2)  =  a2 + b2

12thnewsylabusex2.7q3

Solution

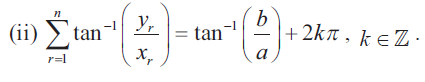
(4)  If (1 + z)/(1 - z)  =  cos 2θ + i sin 2θ, show that z = i tan θ            Solution

(5)  If cos α + cos β + cos γ = sin α + sin β + sin γ = 0, show that

(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) and

(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ) 

Solution

(6)  If z = x + iy and arg [(z - i)/(z + 2)]  =  π/4, show that x2 + y2 + 3x − 3y + 2 = 0.                   Solution

Answer Key

1)  (1/√2)(1 + i)

2)   (-1/2) 

3)  (x12+y12) (x22 + y22)(x32 + y32) ..............(xn2 + y2) =  (a2+b2)

4)  ∑r = 1 to n tan-1(yr/xr) = tan-1(b/a)  + 2kπ, k ∈ z

5)   [-9√3/2 -  i (9/2)]

6)  (1/4) (√2 + i√2)

7)   (√2/2 + i√2/2)

8)  5√2 (cos π/4 + i sin π/4)

9)  2 (cos 5π/6 + i sin 5π/6)

(1)  If z = x + iy is a complex number such that |(z - 4i)/(z + 4i)|  =  1 show that the locus of z is real axis.   Solution

(2)  If z = x + iy is a complex number such that im (2z + 1)/(iz + 1)  =  0, show that locus of z is 2x2 + 2y2 + x - 2y  =  0            Solution

(3)  Obtain the Cartesian form of the locus of z = x + iy in each of the following cases:

(i)  [Re (iz)]2  =  3

(ii)  im [(1 - i)z + 1]  =  0

(iii)  |z + i|  =  |z - 1|

(iv)  z bar  =  z-1                 Solution

(4)  Show that the following equations represent a circle, and, find its centre and radius

(i)  |z - 2 - i|  =  3

(ii) |2z + 2 − 4i| = 2

(iii) |3z − 6 +12i|  =  8.               Solution

(5)  Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases:

(i) |z − 4| = 16

(ii) |z − 4|2 - |z - 1|2 = 16         Solution

Answer Key

1)  Since the value of y is 0, we have shown that locus z is real axis.

2)  2x2 + x - 2y + 2y2  =  0

3)  i)  y2 - 3  =  0    ii) x - y  =  0

iii)  x + y  =  0      iv)  x2 + y2  =  1

4)  

i)   centre and radius are (2, 1) and 3 respectively.

ii)  centre and radius are (-1, 2) and 1 respectively. 

iii)  centre and radius are (2, -4) and 8/3 respectively. 

5)

i)  x2 + y2 - 8x - 240  =  0

ii)  6x + 1  =  0

1)

P represents the variable complex number z, find the locus of P if

Re (z + 1/z + i) = 1

Solution

2)

P represents the variable complex number z, find the locus of P if

|z - 5i|  =  |z + 5i|

Solution

3)

P represents the variable complex number z, find the locus of P if

| 2z − 3 | = 2

Solution

Answer Key

1)  the locus of the given complex number is

x - y - 1  =  0

2)  y  =  0

3)  4x2 + 4y2- 12x + 5  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

©All rights reserved. onlinemath4all.com

Recent Articles

RSS

  1. Digital SAT Math Problems and Solutions (Part - 245)

    Aug 05, 25 07:59 AM

    digitalsatmath354.png
    Digital SAT Math Problems and Solutions (Part - 245)

    Read More

  2. Digital SAT Math Problems and Solutions (Part - 244)

    Aug 04, 25 11:43 AM

    digitalsatmath351.png
    Digital SAT Math Problems and Solutions (Part - 244)

    Read More

  3. Digital SAT Math Problems and Solutions (Part 243)

    Aug 04, 25 07:07 AM

    digitalsatmath349.png
    Digital SAT Math Problems and Solutions (Part 243)

    Read More