COMPLEX NUMBERS PRACTICE PROBLEMS

Complex Numbers Practice Problems :

Here we are going to see some some practice problems on complex numbers.

Complex Numbers Practice Problems

Problem 1 :

If (1 + z)/(1 - z)  =  cos 2θ + i sin 2θ, show that z = i tan θ

Solution :

(1 + z)/(1 - z)  =  cos 2θ + i sin 2θ

1 + z  =  (1 - z)(cos 2θ + i sin 2θ)

1 + z  =  (cos 2θ + i sin 2θ) - z(cos 2θ + i sin 2θ)

z + z(cos 2θ + i sin 2θ)  =  (cos 2θ + i sin 2θ) - 1

z(1 + (cos 2θ + i sin 2θ))  =  (cos 2θ + i sin 2θ) - 1

z = (cos 2θ + i sin 2θ) - 1/(1 + (cos 2θ + i sin 2θ))

z = (cos 2θ - 1) + i sin 2θ)/((1 + cos 2θ) + i sin 2θ))

cos 2θ  =  (1 - tan²θ)/(1 + tan²θ)

sin 2θ  =  2tanθ/(1 - tan²θ)

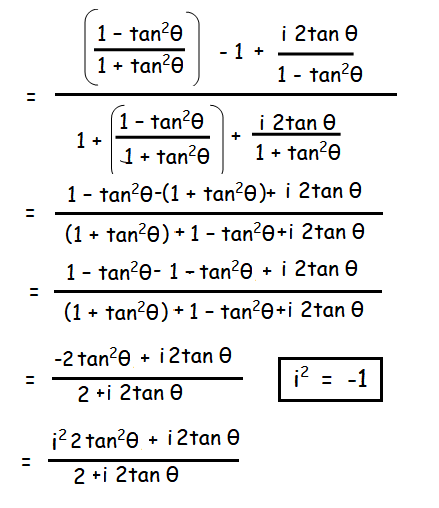
  =  i 2 tan θ (i tan θ + 1)/2(1 + i tan θ)

  =  i tan θ ------- R.H.S

Hence proved.

Problem 2 :

If cos α + cos β + cos γ = sin α + sin β + sin γ = 0, show that

(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) and

(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ) 

Solution :

Let a = cos α + i sin α,

b = cos β + i sin β and c = cos γ + i sin γ

a³  =  (cos α + i sin α)³

b³  =  (cos β + i sin β)³

c³  =  (cos γ + i sin γ)³

Using De moivre's theorem

a³  =  (cos 3α + i sin 3α)  ---(1)

b³  =  (cos 3β + i sin 3β) ---(2)

c³  =  (cos 3γ + i sin 3γ) ---(3)

Algebraic formula :

a³ + b³ + c³  - 3abc  =  (a+b+c) (a² + b² + c² - ab - bc - ca)

If a + b + c = 0, then 

a³ + b³ + c³ = 3abc

Here

a + b + c  =  cos α + i sin α + cos β + i sin β + cos γ + i sin γ

a + b + c  =  (cos α + cos β + cos γ) + i (sin α + sin β + sin γ)

a + b + c  =  0

(1) + (2) + (3)

a³ + b³ + c³   =  3abc

(cos 3α + i sin 3α) + (cos 3β + i sin 3β) +  (cos 3γ + i sin 3γ) 

  =  3 (cos α + i sin α)(cos β + i sin β) (cos γ + i sin γ)

  =  3 [cos (α + β + γ) + i sin (α + β + γ)]

  =  3 cos (α + β + γ) + i 3 sin (α + β + γ)

Equating the real parts, we get

cos 3α + cos 3β + cos 3γ  =  3 cos (α + β + γ)

By equating the imaginary parts, we get 

sin 3α + sin 3β + sin 3γ  =  3 sin (α + β + γ)

Hence proved.

Problem 3 :

If z = x + iy and arg [(z - i)/(z + 2)]  =  π/4, show that x² + y² + 3x − 3y + 2 = 0.

Solution :

arg [(z - i)/(z + 2)]  =  arg (z - i) - arg (z + 2)

  =  arg (x + iy - i) - arg (x + iy + 2)

  =  arg (x + i(y - 1)) - arg ((x + 2) + iy)

  =  tan^-1 [(y - 1)/x] - tan^-1 [y/(x + 2)]

tan^-1 A - tan^-1 B  =  tan^-1 [(A - B)/ (1 + AB)]

Here A = (y - 1)/x and B = y/(x + 2)

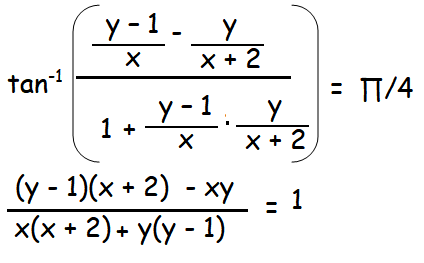
xy + 2y - x - 2 - xy  =  x² + 2x + y² - y

x² + 2x + x + y² - y - 2y + 2  =  0

x²  + y² + 3x - 3y + 2  =  0

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.