CONVERTING COMPLEX NUMBERS TO POLAR FORM

Write the following complex numbers in polar form. 

Problem 1 :

2 + i 2√3

Solution :

2 + i 2√3  =  r (cos θ + i sin θ)

Since the complex number 2 + i 2√3 lies in the first quadrant, has the principal value θ  =  α.

So, the polar form of the given complex number is

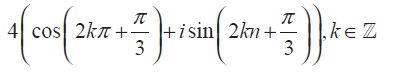
Problem 2 :

3 - i √3

Solution :

3 - i √3  =  r (cos θ + i sin θ)

Since the complex number 3-i√3 lies in the fourth quadrant, has the principal value θ  =  -α.

θ  =  -π/6

3 - i √3  =  2√3 (cos (-π/6) + i sin (-π/6)

3 - i √3  =  2√3 (cos (π/6) - i sin (π/6))

So, the polar form of the given complex number is

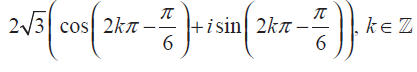
Problem 3 :

-2 - i2

Solution :

−2 − i2  =  r (cos θ + i sin θ)

Since the complex number −2 − i2 lies in the third quadrant, has the principal value θ  =  -π+α.

θ  =  -π + π/4

θ  =  (-4π+π)/4

θ  =  -3π/4

−2 − i2  =  2√3 (cos ( -3π/4) + i sin ( -3π/4))

So, the polar form of the given complex number is

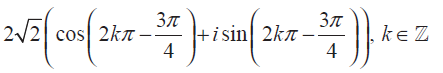
Problem 4 : 

(i - 1) / [cos (π/3) + i sin  (π/3)]

Solution :

=  (i - 1) / [cos (π/3) + i sin  (π/3)]

=  (i - 1) / [(1/2) + i (√3/2)]

=  2(i - 1) / (1 + i√3)

=  (2i - 2) / (1 + i√3)

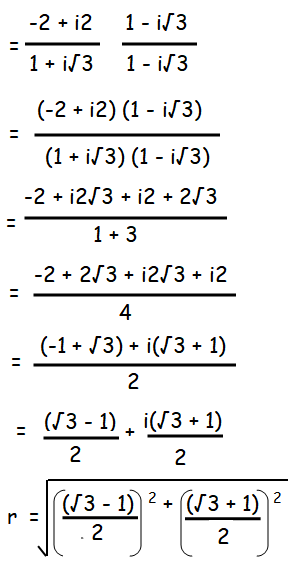
r  =  √[(4 + 2√3 + 4 - 2√3)/4]

r  =  √2

α  = tan^-1|(√3+1)/(√3-1)|

 α  =  tan^-1 (5π/12) 

tan 75  =  tan (30 + 45)

=  (tan 30 + tan 45)/(1 - tan 30 tan 45)

=  [(1/√3) + 1]/[1 - (1/√3)1]

=  (1 + √3)/(√3 - 1)

=  (√3 + 1)/(√3 - 1)

(i - 1) / [cos (π/3) + i sin  (π/3)]

  =  √2 (cos (5π/12)  + i sin (5π/12)) 

So, the polar form of the given complex number is

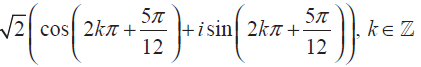
Problem 5 :

(3/2) - i(√3/2)

Solution :

(3/2) - i(√3/2)  =  r (cos θ + i sin θ)

r = √(3/2)² + (√3/2)²

= √(9/4) + (3/4)

= √(9 + 3)/4

= √(12/4)

r = √3

(3/2) - i(√3/2)  = √3 (cos θ + i sin θ)

√3 cos θ = (3/2) and √3 sin θ = √3/2

cos θ = √3/2 and sin θ = 1/2

both sin θ and cos θ are positive, the required angle lies in the first quadrant.

θ = π/6

(3/2) - i(√3/2)  = √3 (cos π/6 + i sin π/6)

Problem 6 :

-1 - i√3

Solution :

-1 - i√3 =  r (cos θ + i sin θ)

r = √(-1)² + (-√3)²

= √1 + 3

= √4

r = 2

-1 - i√3  = 2 (cos θ + i sin θ)

2 cos θ = -1 and 2 sin θ = -√3

cos θ = -1/2 and sin θ = -√3/2

both sin θ and cos θ are positive, the required angle lies in the third quadrant.

θ = -π + a

= -π + (π/3)

= (-3π + π)/3

= -2π/3

-1 - i√3 = 2 (cos (-2π/3) + i sin (-2π/3))

Problem 7 :

-2√3 - 2i

Solution :

-2√3 - 2i =  r (cos θ + i sin θ)

r = √(-2√3)² + (-2)²

= √12+4

= √16

r = 4

-2√3 - 2i  = 4 (cos θ + i sin θ)

4 cos θ = -2√3 and 4 sin θ = -2

cos θ = -√3/2 and sin θ = -1/2

both sin θ and cos θ are positive, the required angle lies in the third quadrant.

θ = -π + a

= -π + (π/6)

= -5π/6

-2√3 - 2i  = 2 (cos (-5π/6) + i sin (-5π/6))

Problem 8 :

2i

Solution :

2i =  r (cos θ + i sin θ)

r = √0² + 2²

= √4

r = 2

2i  = 2 (cos θ + i sin θ)

2 cos θ = 0 and 2 sin θ = 2

cos θ = 0 and sin θ = 2/2

cos θ = 0 and sin θ = 1

both sin θ and cos θ are positive, the required angle lies in the first quadrant.

θ = a

= π/2

2i  = 2 (cos (π/2) + i sin (π/2))

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.