HOW TO FIND LOCUS OF COMPLEX NUMBERS

Example 1 :

P represents the variable complex number z, find the locus of P if

Re (z + 1/z + i) = 1

Solution :

Let z = x + iy then

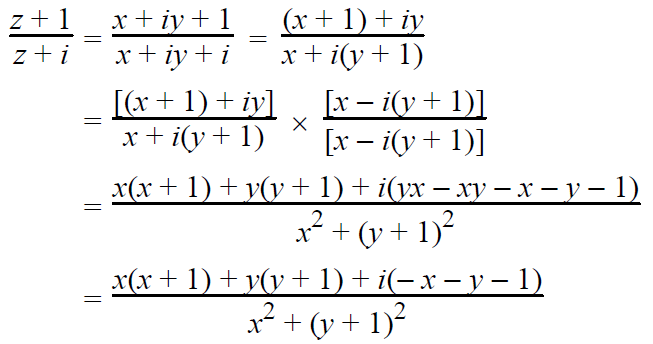
By equating the real part of te complex number to 1, we get

[x (x + 1) + y (y + 1)]/x² + (y + 1)²  =  1

(x² + x + y² + y)/x² + (y + 1)²  =  1

(x² + y² + x + y)/(x² + (y² + 2y + 1)) =  1

(x² + y² + x + y)/(x² + y² + 2y + 1) =  1

x² + y² + x + y  =  x² + y² + 2y + 1 

x² - x² + y² - y² + x + y - 2y - 1  =  0

x - y - 1  = 0

So, the locus of the given complex number is

x - y - 1  =  0

Example 2 :

P represents the variable complex number z, find the locus of P if

|z - 5i|  =  |z + 5i|

Solution :

Let z = x + iy then

|z - 5i|  =  |z + 5i|

|(x + iy) - 5i|  =  |(x + iy) + 5i|

|x + i(y - 5)|  =  |x + i(y + 5)|

√x² + (y - 5)²   =  √x² + (y + 5)²

Taking squares on both sides

x² + (y - 5)²   =  x² + (y + 5)²

x² + y² - 10y + 25   =  x² + y² + 10y+ 25

x² + y^{2 -} x^{2 -} y² - 10y - 10 y + 25 - 25   =  0

-20y  =  0

y  =  0 

So, the locus of given complex number is

y  =  0

Example 3 :

P represents the variable complex number z, find the locus of P if

| 2z − 3 | = 2

Solution :

Let z = x + iy then

| 2z − 3 | = 2

| 2(x + iy) − 3 | = 2

| 2x + i2y − 3 | = 2

| (2x − 3) + i 2y | = 2

√(2x − 3)² + (2y)² = 2

Taking squares on both sides

(2x)² - 2(2x)(3) + 3² + (2y)² = 2²

4x² - 12x + 9 + 4y² = 4

4x² + 4y²- 12x + 9 - 4  =  0

4x² + 4y²- 12x + 5  =  0

So, the locus of given complex number is 

4x² + 4y²- 12x + 5  =  0

Example 4 :

On a sketch of argand diagram, show the locus representing complex numbers satisfying the equation : 

|z| = |z - 4 - 3i|

Solution :

|z| = |z - 4 - 3i|

Let z = x + iy

|x + iy|  = |x + iy - 4 - 3i|

|x + iy|  = |(x - 4) + i(y - 3)|

On both side of the equal sign, since we have absolute sign, we find the modulus.

√x² + y² = √(x - 4)² + (y - 3)²

x² + y² = (x - 4)² + (y - 3)²

x² + y² = x² - 2(x)(4) + 4² + y² - 2y(3) + 3²

x² + y² = x² - 8x + 16 + y² - 6y + 9

x²  + y²  - 8x- 6y + 9 + 16 = 0

x²  + y² - 8x- 6y + 25 = 0

Example 5 :

The point P represents a complex number z on the Argand plane 

|z - w⁶| = 3 |z - w⁶|

Solution :

Where 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.