SAT Math Practice Questions with Answers

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Question 1 :

A circle has center A, and points B and C lie on the circle. Line segments BD and CD are tangent to the circle at points B and C, respectively. The measure of angle BDC is 120°. The length of line segment CD is 12 inches. What is the area of the region that is both inside the quadrilateral ABCD and outside the circle, in square inches? (Round your answer to the nearest hundredth of a square inch)

Answer :

Question 2 :

If 4k – x is a factor of x³ – 72nk³, where n and k are constants and k > 0, what is the value of n?

Answer :

Question 3 :

The numbers a, b, c, p and w are positive constants, where b > c. The number a is 1,150% more than the positive difference between b and c, and c is 50% of b. If a is p% greater than c, and c is w% of a, what is the value of pw?

Answer :

Question 4 :

(10b + 6a)x² + (9a² – 25b²)x – 12ab = 0

The equation above has two real solutions, where a and b are constants. The sum of the solutions to the given equation is k(21a – 35b), where k is a constant. What is the value of k?

Answer :

Question 5 :

Ramachandran invented a new temperature scale he called the Onlinemath4all scale. The function T gives the temperature, in degree Torte, that corresponds to a temperature of x degrees Celsius. If a temperature increased by 3.3 degree Torte, by how much did the temperature increase, in degrees Celsius? Round your answer to the nearest hundredth.

Answer :

Question 6 :

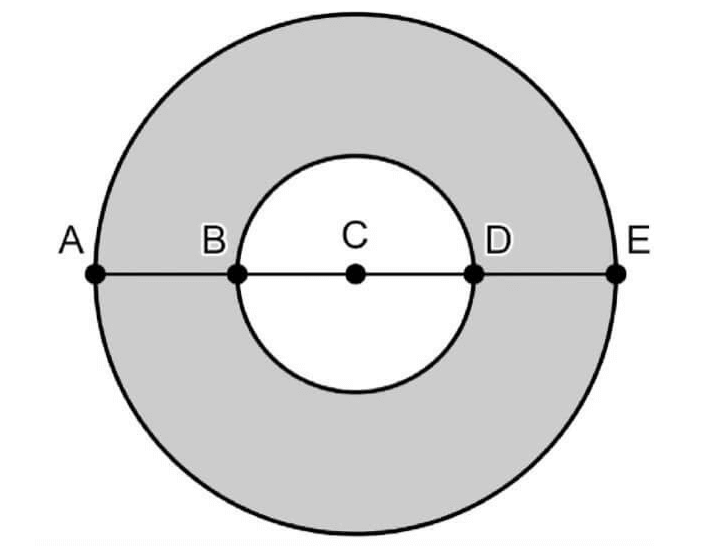
In the figure shown, point C is the center of both circles. The ratio of AB to CD is 6 to 5. If the area of the larger circle is 242, what is the area of the shaded region?

Answer :

Question 7 :

a(x – 5) + 4b = 7(b – 5x)

The equation above has no solution, where a and b are constants. The number b CANNOT be equal to the number m. What is the value of m? Round your answer to the nearest hundredth.

Answer :

Question 8 :

A fruit orchard has 8 rows of apple trees and 4 rows of orange trees. Each row of apple trees has 15 trees that are healthy and 6 trees that are unhealthy. Each row of orange trees has 10 trees that are healthy and 2 trees that are unhealthy. The probability of selecting an apple tree, given that that the tree is unhealthy, is equal to w. The probability of selecting an unhealthy tree , given that the tree is an orange tree, is equal to z. Note that w and z are positive constants. What is the positive difference between w and z? Round your answer to the nearest hundredth.

Answer :

Question 9 :

(3x – 7p)(5x² + 8x – 4p)(x³ + 3x² – 16x – 48) = 0

In the given equation, p is a positive constant. The product of the solutions to the equation is –560/9. What is the value of p?

Answer :

Question 10 :

In triangles ABC and JKL, angles B and K each have a measure of 44°. The length of side BC and the length of side KL are both equal to 25. Which additional piece of information is sufficient to prove that triangle ABC is congruent to triangle JKL?

A) The length of side AC is 13 and the length of side JL is 13.

B) The measure of angle A is 58° and the measure of angle L is 58°.

C) The measure of angle A is 37° and the measure of angle J is 37°.

D) No additional information is necessary.

Answer :

Question 11 :

If k – x is a factor of –x² + (1/29)nk², where n and k are constants and k > 0, what is the value of n?

A) –29

B) – 1/29

C) 1/29

D) 29

Answer :

Question 12 :

In triangle ABC, sin ∠A = cos ∠B. If m∠A = (6y – 1)°, m∠B = (8y + 7)° and m∠C = (2x + y)°, what is the value of x?

Answer :

Question 13 :

John can complete a job in 20 minutes. Bob can complete the same job in 40 minutes. If they work together, approximately how many minutes will it take them to complete the job?

A) 60 minutes

B) 40 minutes

C) 30 minutes

D) 15 minutes

Answer :

Question 14 :

f(x) = –2x² + jx – 5

g(x) = 2x² + kx + 7

For the two functions above, f(x) has its maximum value and g(x) has its minimum value for the same value of x. What is the value of j + k?

Answer :

Question 15 :

Two spheres have radii in the ratio 12 : 13. The difference in their surface areas is 400π square inches. If the volume of the smaller sphere can be written as vπ, what is the value of v?

Answer :

Question 16 :

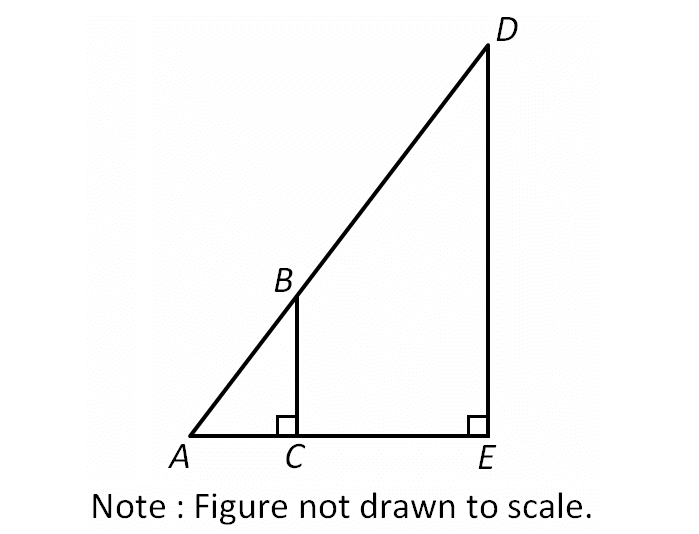
In the figure shown, AB = √185 units, AC = 4 units and CE = 10 units. What is the area, in square units, of triangle ADE?

Answer :

Question 17 :

The function q is defined by

q(x) = a|x – 9|² – 53|x – 9|+ b

where a and b are constants, and a > b > 53. If q(539) = h and q(–521) = k, where h and k are constants, what is the value of

32(–539)^h^{– k} + 347(9)^k^{– h} ?

Answer :

Question 18 :

A bird-watching group initially observed 200 birds in a certain area and set a goal of reaching 800 birds. According to their model, the population starts at 200 and increases by 30 birds per week for the first two weeks after the observation. After those two weeks, the population increases by 50 birds per week until the goal of 800 birds is reached. At the end of week w (where w > 2) after the initial observation, let p(w) be the predicted number of birds still needed to reach the 800-bird goal. Which of the following functions correctly represents p(w)?

A) p(w) = 800 – 50w

B) p(w) = 750 + 50w

C) p(w) = 640 – 50w

D) p(w) = 260 + 50w

Answer :

Question 19 :

A circle in the xy-plane has its center at (2, –3) and has a radius of 7. An equation of this circle is x² + y² + ax + by + c = 0, where a, b and c are constants. What is the value of c?

Answer :

Question 20 :

A circle has center G, and points M and N lie on the circle. Line segments MH and NH are tangent to the circle at points M and N, respectively. If the radius of the circle is 150 millimeters and the perimeter of quadrilateral GMHN is 3,500 millimeters, what is the distance, rounded to the nearest millimeter, between points G and H?

A) 150

B) 1,600

C) 1,607

D) 1,617

Answer :