Challenging SAT Math Problems

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Question 1 :

2√a + 3√b = 7√b, where a > 0 and b > 0, what is a in terms of b?

A) 2√b

B) 4√b

C) 2b

D) 4b

Answer :

Problem 2 :

A 100 gram metal alloy is 40% silver. It contains a metal alloy that is 65% silver and a second metal alloy made up of 25% silver. What is the mass of the first metal alloy?

Solution :

Problem 3 :

Joshua Tree National Park has an area of 1,242 square miles. What is the area, in square yards, of Joshua Tree National Park? ( 1 mile = 1,760 yards).

A) 1,242/1,760

B) 1,242/(1,760)²

C) 1,242(1,760)

D) 1,242(1,760)²

Solution :

Problem 4 :

There are two ranches. Ranch A and ranch B. The ratio of male horses to female horses is 1: 15 for the total number of horses on ranch A and B. The ratio of female horses on ranch A to ranch B. is 7: 17. There are 168 horses on ranch A and 344 horses on Ranch B. How many more male horses are there on ranch A than on ranch B?

Solution :

Problem 5 :

A certain bacterial colony currently has 5,000 spores. If the number of spores in this colony quadruples every 33 hours, which of the following functions p gives the number of spores in the colony d days from now?

A) N(d) = 5,000(4)¹¹^d^/8

B) N(d) = 5,000(4)⁸^d^/11

C) N(d) = 5,000(4)⁵^d^/4

D) N(d) = 5,000(4)⁴^d^/5

Solution :

Problem 6 :

In the given equations, a and b are constants, a is greater than 1 and b is greater than 1. What is the value of x?

⁷√a⁵ = √b⁵

a^{3x - 3} = b³

Solution :

Problem 7 :

a is 3700% greater than b. a is also 5% less than c. What percent greater than c is b?

Solution :

Problem 8 :

The proposal for a development project was included on a city’s election ballots. A local tv station reported that 6 times as many people voted in favor of the proposal as people who voted against it. If 1,770 more people voted in favor of the proposal than those who voted against the proposal. How many people voted against the proposal?

Solution :

Problem 9 :

The table gives the volume and surface area of two similar rectangular prisms A and B, where k is a constant. What is the value of k?

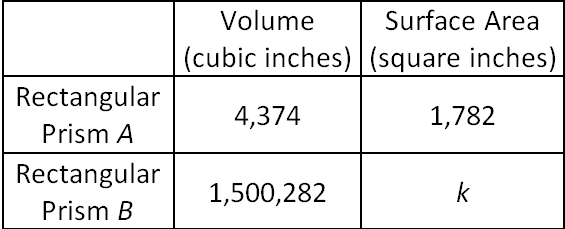
A) 5,346

B) 12,474

C) 87,318

D) 611,226

Solution :

Problem 10 :

In the given system of equations, c is a constant. The system has two distinct real solutions. Which of the following could be the value of c?

y = x - c

y = -6(x - 5)²

A) 2

B) 4

C) 119/24

D) 7

Solution :

Problem 11 :

The function f is defined by f(x) = a√(x + b), where a and b are constants and a ≠ 0. In the xy-plane, the graph of y = f(x) passes through the point (–24, 0), and f(24) < 0. Which of the following must be true?

A) f(0) = 24

B) f(0) = -24

C) a > b

D) a < b

Solution :

Problem 12 :

The function f is defined by f(x) = a(2.2^x + 2.2^b), where a and b are integer constants and 0 < a < b. The functions g and h are equivalent to function f, where k and m are constants. Which of the following equations displays the y-coordinate of the y-intercept of the graph of y = f(x) in the xy-plane as a constant or coefficient?

I. g(x) = a(2.2^x + k)

II. h(x) = a(2.2)^x + m

A) I only

B) II only

C) I and II

D) Neither I nor II

Solution :

Problem 13 :

h(x) = 5(x – m)(x – n)(x – r)

The function h is defined by the given equation, where m, n and r distinct constants. When m < x < r, the value of h(x) is positive. The graph of y = h(x) constains the point (s, t), where s and t are constants. If t = 9, which of the following could be true?

I. n < s

II. s < m

III. r < s < n

A) I only

B) II only

C) III only

D) None of them

Solution :

Problem 14 :

-19(6x - 4)² + 6(6x - 3)²

The given expression can be rewritten as (a/9)x² + (b/9)x + c/9, where a, b and c are constants. What is the value of a + b + c?

Solution :

Problem 15 :

A rectangular area consists of 3,179 equal squares where each square has an area of k. If the length of the rectangular area is 2.75 times the width and the width is equal to x√k, what is the value of x?

Solution :

Problem 16 :

f(x) = x² + 5x - 6

g(x) = x² + 2x - 35

The quadratic function f(x) has 2 solutions j and k, where j < k. The quadratic function g(x) has 2 solutions ℓ and m, where ℓ < m. The quadratic function h(x) = x² + 7x + c has solutions of k + ℓand m + j, and can be rewritten as (x + a)(x + b), what is the value of c?

Solution :

Problem 17 :

For the exponential function f(x) = 16^x^{+ 4}, which of the following answer choices expresses the minimum value as either a constant or coefficient when x ≥ 0?

A) f(x) = 64(16)^x

B) f(x) = 65,536(16)^x

C) f(x) = 1,048,576(16)^x

D) (1/65,356)(16)^x

Solution :

Problem 18 :

For the given parabola f(x) = ax² + bx + c, a, b and c are constants. The x-intercepts of the parabola are at (14, 0) and (k, 0). If f(27) = f(11), what is the value of k?

Solution :

Problem 19 :

A quadratic function models a projectile’s height, in meters, above the ground in terms of time, in seconds, after it was launched. The model estimates that the projectile was launched from an initial height of a meters and reached a maximum height of 134 meters 6 seconds after it was launched. How many seconds after launch does the model estimate it will return to a height of a meters?

A) 6

B) 8

C) 9

D) 12

Solution :

Problem 20 :

M(t) = 10(½)^t/5730

The function M models the mass of the radioactive isotope carbom-14 in a sample, in picograms, t years after the initial measurement. How much time, in years, does it take for the mass of carbon-14 in the sample to decrease to 5 picograms?

Solution :