How to Solve the Hardest SAT Math Problems

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Solving the hardest Math problems in SAT requires deep understanding of the core concepts in Algebra, Geometry and Trigonometry. Mastering Desmos for graphing, plugging in answer choices (backsolving), and recognizing complex algebraic patterns. Going over the following hard SAT Math problems will help the students to improve their scores in SAT Math section.

Problem 1 :

The positive number a is 520% of the number b, and a is 65% of the number c. If c is p% of b, which of the following is the value of p?

A) 3.38

B) 8

C) 338

D) 800

Solution :

Problem 2 :

For the exponential function g, the value of g(3) is q, where q is a constant. Which of the following equivalent forms of the function g shows the value of q as the coefficient or the base?

A) g(x) = 27(1.2)^x^{+ 3}

B) g(x) = 64(1.2)^x^{- 1}

C) g(x) = 172(1.2)^x

D) g(x) = 1036(1.2)^x^{– 3}

Solution :

Problem 3 :

Let f(x) = 42(a/21)^{x + b} + c.

How many times does the graph of the given function in the xy-plane cross the x-axis, where a, b and c are integer constants such that a > 21, b < 0 and c < b?

A) Zero

B) Once

C) Twice

D) Three

Solution :

Problem 4 :

x² + 10x + y² + 12y – 723 = 0

In the xy-plane, the graph of the given equation is a circle. If this circle is inscribed in a square, what is the perimeter of the square?

Solution :

Problem 5 :

A right circular cone has a volume of 2592π cubic inches, and the area of its base is 324π square inches. What is the slant height, in inches, of this cone?

Solution :

Problem 6 :

The area of a triangle is equal to x² square inches. The base of the triangle is 21 – x inches, and the height of the triangle is 4 – x inches. Which of the following could be the value of x?

A) –28

B) –3

C) 1/2

D) 2

Solution :

Problem 7 :

The table gives the volume of two similar cylinders. If the radius of cylinder A is 6 cm, what is the value of r – s?

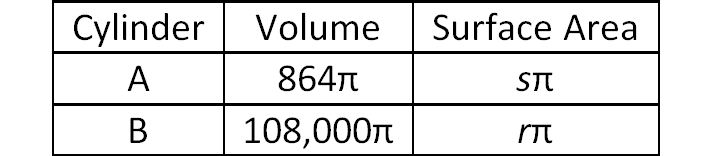
volume = πr²h

surface area = 2πr² + 2πrh

Solution :

Problem 8 :

In triangle ABC, angle C is a right angle, point D lies on AB, point E lies on BC, and DE is parallel to AC. If the length of AB is 39 units, DE is 8 units, the length of AC is greater than the length of BC, and the area of the triangle ABC is 270 square units, what is the length of BE, in units?

Solution :

Problem 9 :

If k = ℓ + m, which of the following is equivalent to the expression x² – ℓ² – 2ℓm – m²?

A) (x + k)²

B) (x – k)²

C) (x + k)(x – k)

D) x² – kx – k²

Solution :

Problem 10 :

In the equation below, k is a constant. What is the value of k, if the equation has one solution?

¼|x – 4| – 30 = 2k

Solution :

Problem 11 :

What is the value of x in the equation above?

Answer :

Question 12 :

For the quadratic function y = f(x), (x – 3) is a factor and x = k is a positive zero. If (5, c) is the maximum point on the graph of y = f(x), what is the value of k?

Answer :

Question 13 :

Which of the following expresses a in terms of b and c?

Answer :

Question 14 :

The function f is defined by f(2x – 1) = 4x + 3 and the function g is defined by g(x) = f(x) – 1. What is the value of g(10)?

Answer :

Question 15 :

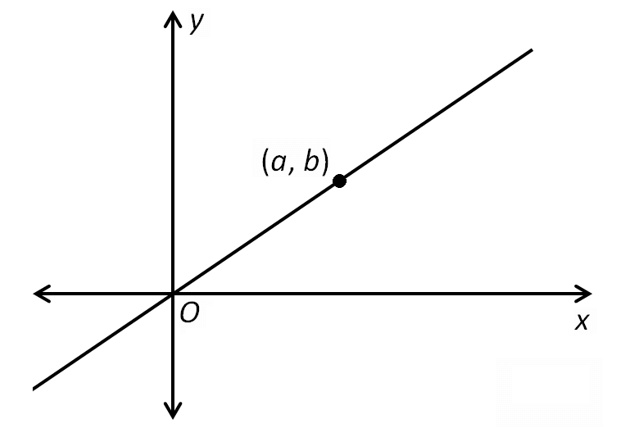
The line shown in the xy-plane passes through the point (0, 0) and the point (a, b), where a > b. Which of the following could be the slope of this line?

A) -1/2

B) 3/4

C) 1

D) 3/2

Answer :

Question 16 :

A rectangle is inscribed in a circle, such that each vertex of the rectangle lies on the circumference of the circle. The diagonal of the rectangle is twice the length of the shortest side of the rectangle. The area of the rectangle is 1,089√3 square units. What is the length, in units, of the diameter of the circle?

Answer :

Question 17 :

Rectangles ABCD and EFGH are similar. The length of each side of EFGH is 6 times the length of the corresponding side of ABCD. The area of ABCD is 54 square units. What is the area, in square units, of EFGH?

A) 9

B) 36

C) 324

D) 1,944

Answer :

Question 18 :

P(t) = 260(1.04)^(6/4)^t

The function P models the population, in thousands, of a certain city t years after 2003. According to the model, the population is predicted to increase by 4% every n months. What is the value of n?

A) 8

B) 12

C) 18

D) 72

Answer :

Question 19 :

A circle in the xy-plane has its center at (-1, 1). Line t is tangent to this circle at the point (5, -4). Which of the following points also lies on line t?

A) (0, 6/5)

B) (4, 7)

C) (10, 2)

D) (11, 1)

Answer :

Question 20 :

For an electric field passing through a flat surface perpendicular to it, the electric flux of the electric field through the surface is the product of the electric field’s strength and the area of the surface. A certain flat surface consists of two adjacent squares, where the side length, in meters, of the larger square is 3 times the side length, in meters, of the smaller square. An electric field with strength 29.00 volts per meter passes uniformly through this surface, which is perpendicular to the electric field. If the total electric flux of the electric field through this surface is 4,640 volts · meters, what is the electric flux, in volts · meters, of the electric field through the larger square?

Answer :