PRACTICE QUESTIONS ON MATRICES WORKSHEET FOR GRADE 11

(1)  Construct an m × n matrix A  =  [a_ij], where a_ij is given by 

(i)  a_ij  =  (i - 2j)²/2 with m = 2 and n = 3      Solution

(ii)  a_ij  =  |3i - 4j|/4 with m = 3 and n = 4     Solution

(2)  Find the values of p, q, r, and s if

Solution

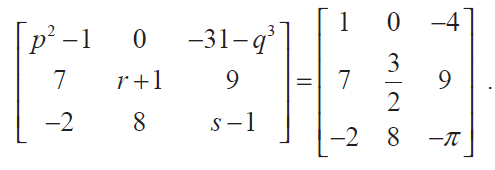
(3)  Determine the value of x + y if

Solution

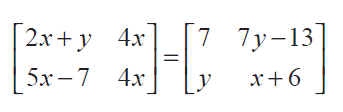
(4)  Determine the matrices A and B if they satisfy

Solution

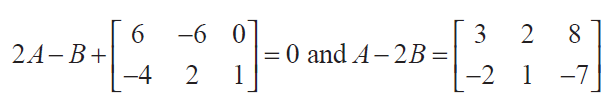
(5)  If A  =  

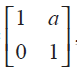
then compute A⁴              Solution

(6)  Consider the matrix

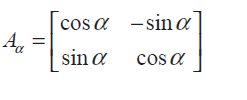
(i)  Show that A_α A_β =  A_(α+β)

(ii) Find all possible real values of α satisfying the condition A_{α +} A_α^T  =  I      Solution

(7)  If A  =  

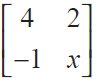
and such that (A− 2I)(A− 3I) = O, find the value of x.

Solution

(8)  If A =  

Solution

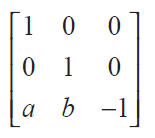
(9)  If A  =  

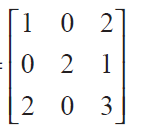
and A³ - 6A² + 7A + KI  =  0, then find the value of k.

Solution

(10)  Give your own examples of matrices satisfying the following conditions in each case:

(i) A and B such that AB ≠ BA .

(ii) A and B such that AB = O = BA, A ≠ O and B ≠ O.

(iii) A and B such that AB = O and BA ≠ O.  

Solution

(11)  Show that f (x) f ( y) = f (x + y), where f(x)  =  

Solution

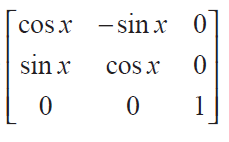
(12)  If A is a square matrix such that A² = A, find the value of 7A - (I + A)³.        Solution

(13)  Verify the property A(B + C) = AB + AC, when the matrices A, B, and C are given by

Solution

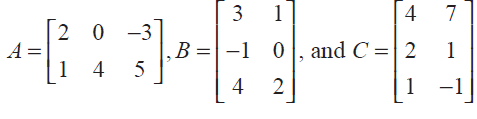
(14)  Find the matrix A which satisfies the matrix relation 

Solution

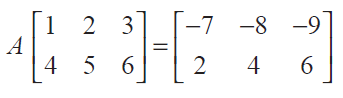
(15)  

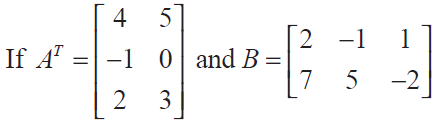
verify the following (i) (A+ B)^T = A^T + B^T = B^T + A^T

(ii) (A− B)^T = A^T − B^T

(iii) (B^T )^T = B .

Solution

(16)  If A is a 3 × 4 matrix and B is a matrix such that both A^T B and BA^T are defined, what is the order of the matrix B?         Solution

(17)  Express the following matrices as the sum of a symmetric matrix and a skew-symmetric matrix:

Solution 

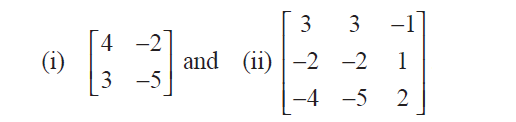
(18)  Find the matrix A such that

Solution

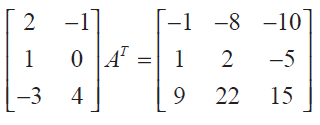
(19)  If A

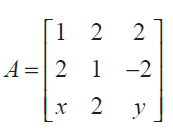
is a matrix such that AA^T = 9I , find the values of x and y.       Solution

(20)  (i)  For what value of x, the matrix

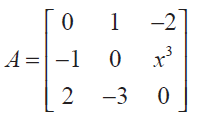
is skew-symmetric     Solution

(ii)  If A  =

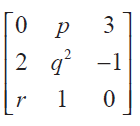
is skew-symmetric, find the values of p, q, and r.

Solution

(21)  Construct the matrix A  =  [a_ij]_3x3, where a_ij  =  i - j. State whether A is symmetric or skew-symmetric

Solution

(22)  Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix.

Solution

(23)  If A and B are symmetric matrices of same order, prove that

(i) AB + BA is a symmetric matrix.

(ii) AB - BA is a skew-symmetric matrix     Solution

(24)  A shopkeeper in a Nuts and Spices shop makes gift packs of cashew nuts, raisins and almonds.

Pack I contains 100 gm of cashew nuts, 100 gm of raisins and 50 gm of almonds.

Pack-II contains 200 gm of cashew nuts, 100 gm of raisins and 100 gm of almonds.

Pack-III contains 250 gm of cashew nuts, 250 gm of raisins and 150 gm of almonds.

The cost of 50 gm of cashew nuts is $50, 50 gm of raisins is $10, and 50 gm of almonds is $60. What is the cost of each gift pack?              Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.