PRACTICE QUESTIONS ON TRANSPOSE OF MATRIX

Transpose of a Matrix :

The transpose of a matrix is obtained by interchanging rows and columns of A and is denoted by A^T.

More precisely, if [a_ij] with order m x n, then AT  =   [b_ij] with order n x m,  where b_ij  =  a_ji so that the (i, j)th entry of A^T is  a_ji

We state a few basic results on transpose whose proofs are straight forward.

For any two matrices A and B of suitable orders, we have

(i) (A^T )^T = A

(ii) (kA)^T = kA^T (where k is any scalar)

(iii) (A+ B)^T = A^T + B^T

(iv) (AB)^T = B^T A^T (reversal law on transpose)

Question 1 :

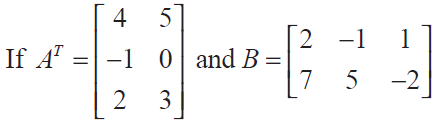
verify the following (i) (A+ B)^T = A^T + B^T = B^T + A^T

(ii) (A− B)^T = A^T − B^T

(iii) (B^T )^T = B .

In order to find the value of (A + B)^T , first let us find the value of A. For that we have to find the transpose of matrix A.

By finding transpose for the transposed matrix, we get the original matrix.

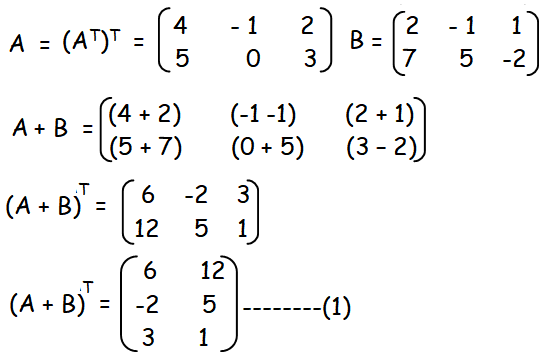
To find the value of A^T + B^T, we have to add those matrices.

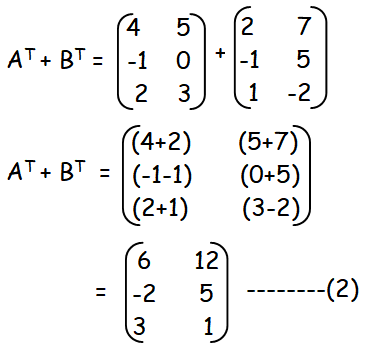
To find the value of B^T+ A^T, we have to add those matrices.

Hence proved.

(ii) (A− B)^T = A^T − B^T

L.H.S

First let us subtract the matrix B from A.Now by interchanging rows and columns, we get (A - B)^T

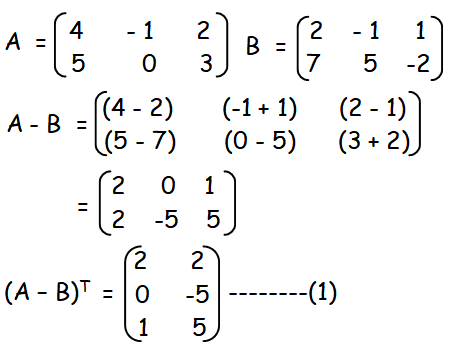
R.H.S

Now we have to subtract B^T from A^T

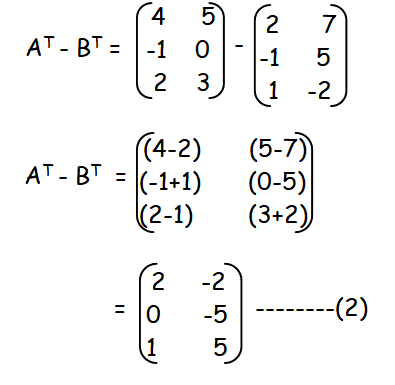
Question 2 :

If A is a 3 × 4 matrix and B is a matrix such that both A^T B and BA^T are defined, what is the order of the matrix B?

Solution :

If A is a matrix of order 3 x 4, then the order of the matrix A^T will be 4 x 3. Since A^T B is defined, matrix B will have the order 3 x 2 or 3 x 1.

If we take the order 3 x 2 for the matrix B, we cannot find the value of BA^T

If the product of two matrices is defined , then the number of columns in the first matrix will be equal to the number of rows in the second matrix.

Hence the required order must be 3 x 4.

So, A^T B will have the order 4 x 4 and the matrix BA^T will have the order 3 x 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.