MATRIX MULTIPLICATION QUESTIONS AND ANSWERS

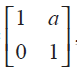then compute A⁴

Solution : 

A⁴  =  A ⋅ A ⋅ A ⋅ A

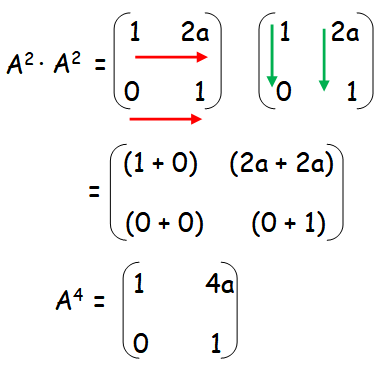
  =  A² ⋅ A²

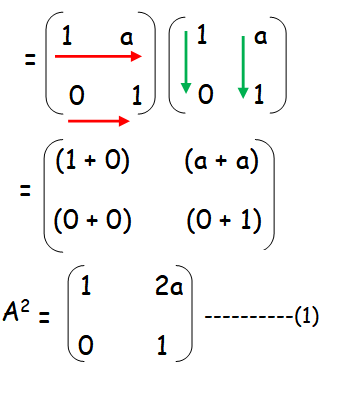
In order to find A⁴, let us multiply A² and A²

Question 2 :

Consider the matrix

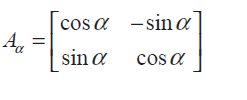
(i)  Show that A_α A_β =  A_(α+β)

(ii) Find all possible real values of α satisfying the condition A_{α +} A_α^T  =  I

Solution :

From the given question, if 

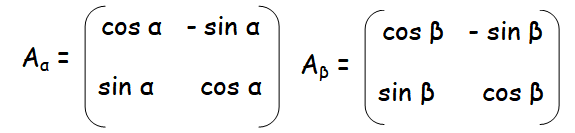
By multiplying A_α A_β, we get

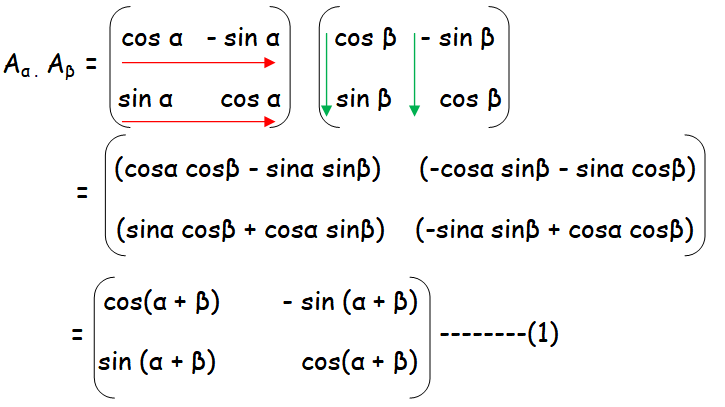
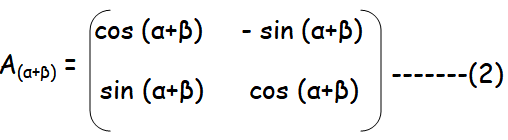
In the given question, by replacing α by (α + β), we get

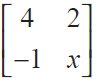and such that (A− 2I)(A− 3I) = O, find the value of x.

Solution :

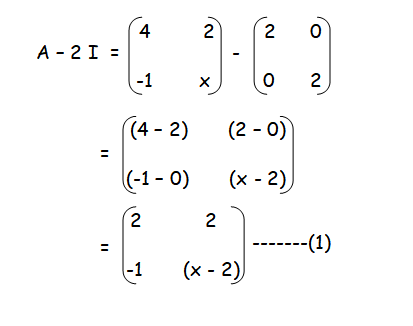
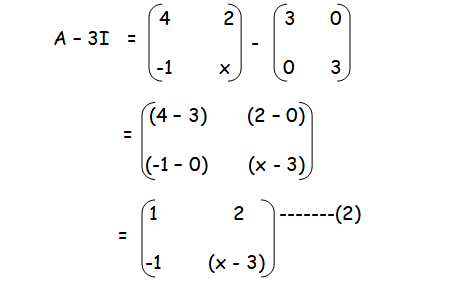
(A− 2I)(A− 3I) = O

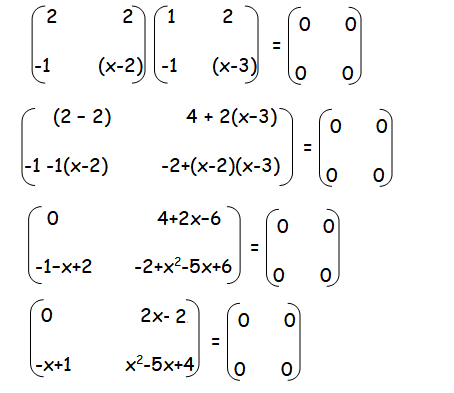
By equating the corresponding terms, we get

2x - 2  = 0

x  =  2/2  =  1

Hence the value of x is 1.

Question 4 :

If A =

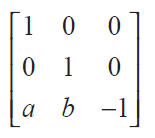
show that A² is a unit matrix.

Solution :

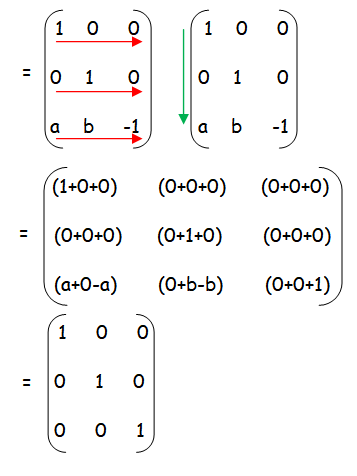
Question 5 :

If A =

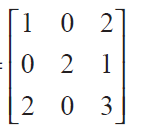
and A³ - 6A² + 7A + KI  =  0, then find the value of k.

Solution :

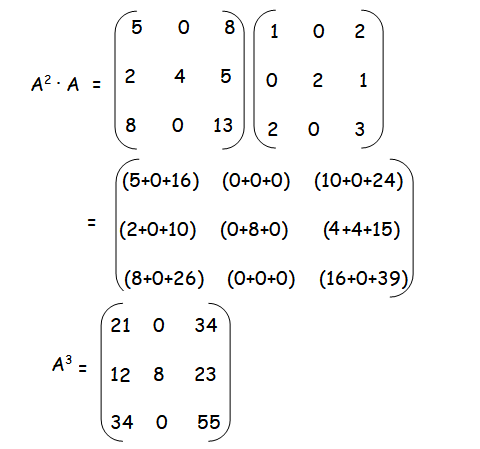
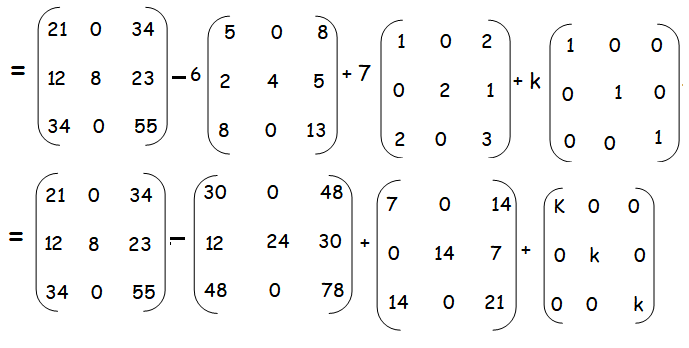
21 - 30 + 7 + K  =  0

28 - 30 + k  =  0

-2 + k  =  0

k  =  2

The value of k is 2.

Question 6 :

Give your own examples of matrices satisfying the following conditions in each case:

(i) A and B such that AB ≠ BA .

(ii) A and B such that AB = O = BA, A ≠ O and B ≠ O.

(iii) A and B such that AB = O and BA ≠ O.

Question 7 :

Show that f (x) f ( y) = f (x + y), where f(x)  =  

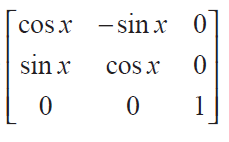
Solution :

Let us find the product of f(x) and f(y)

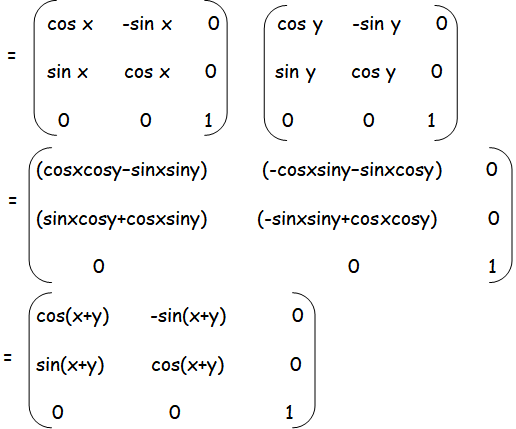
  =  f(x + y)

Hence proved.

Question 8 :

If A is a square matrix such that A² = A, find the value of 7A - (I + A)³.

Solution :

   =  7A - (I + A)³

  =  7A - (I³ + 3A²I + 3AI² + A³)

  =  7A - (I + 3AI + 3AI + A² ⋅ A)

The product of identity matrix and A is matrix A.

 =  7A - (I + 3A + 3A + A ⋅ A)

  =  7A - (I + 6A + A²)

  =  7A - (I + 6A + A)

  =  7A - (I + 7A)

  =  7A - I - 7A

  =  - I

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.