EXAMPLE FOR SKEW SYMMETRIC MATRIX

What is symmetric and skew symmetric matrix ?

For any square matrix A with real number entries, A+ A^T is a symmetric matrix and A− A^T is a skew-symmetric matrix.

Any square matrix can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix.

Let A be a square matrix. Then, we can write

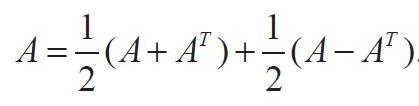
Question 1 :

If A

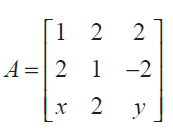
is a matrix such that AA^T = 9I , find the values of x and y.

Solution :

From the given matrix A, first let us find the transpose of matrix A^T.

Here I stands for identity matrix with order 3 x 3.

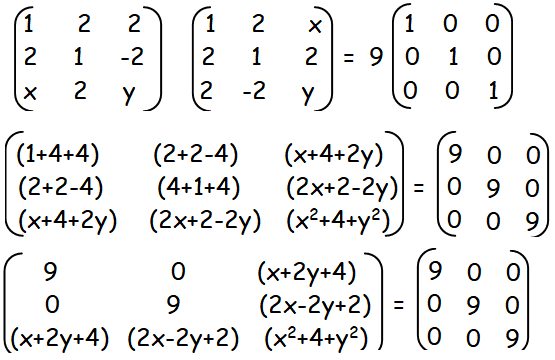
By equating the corresponding terms, we get

x + 2y + 4  =  0   ------(1)

2x - 2y + 2  =  0   ------(2)

By adding the first and second equation, we may eliminate Y.

(x + 2y + 4) + (2x - 2y + 2)  =  0 + 0

x + 2x + 4 + 2  =  0 

3x + 6  =  0

3x  =  -6

 x  =  -6/3  =  -2

So, the value of x is -2.

Now we have to apply the value of x in the first equation, we may get y.

-2 + 2y + 4  =  0

2 + 2y  =  0

2y  =  -2

y  =  -1

Hence the values of x and y are -2 and -1 respectively.

Question 2 :

For what value of x, the matrix

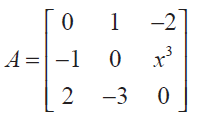
is skew-symmetric

Solution :

A square matrix A is said to be skew-symmetric if A^T = −A.

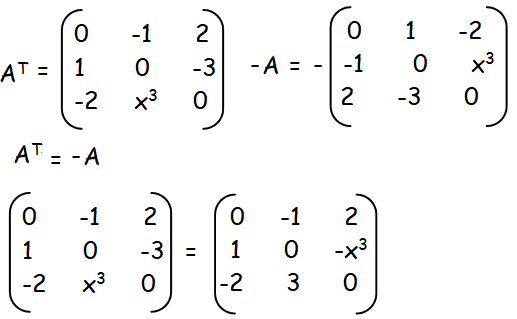
By equating the corresponding terms, we get the value of x.

-3  =  -x³

x³  =  3

x  =  3^1/3

Hence the value of x is 3^1/3.

Question 3 :

If A  =  

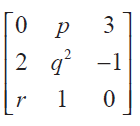
is skew-symmetric, find the values of p, q, and r.

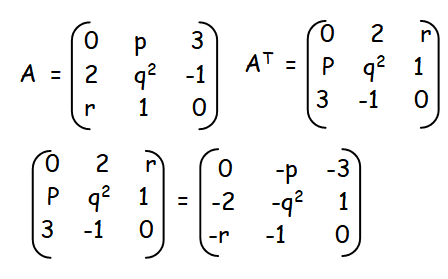
By equating the corresponding values, we may find the values of p, q and r respectively.

Hence the values of p, q and r are -2, 0 and -3 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.