QUESTIONS ON SYMMETRIC AND SKEW SYMMETRIC MATRIX
What is symmetric and skew symmetric matrix ?
A square matrix A is said to be symmetric if AT = A.
A square matrix A is said to be skew-symmetric if AT = −A.
Let us look into some problems to understand the concept.
Question 1 :
Construct the matrix A = [aij]3x3, where aij = i - j. State whether A is symmetric or skew-symmetric
Solution :
From the given question, we come to know that we have to construct a matrix with 3 rows and 3 columns.
|
i = 1, j = 1 aij = i - j a11 = 1 - 1 a11 = 0 |
i = 1, j = 2 aij = i - j a12 = 1 - 2 a12 = -1 |
i = 1, j = 3 aij = i - j a13 = 1 - 3 a13 = -2 |
|
i = 2, j = 1 aij = i - j a21 = 2 - 1 a21 = 1 |
i = 2, j = 2 aij = i - j a22 = 2 - 2 a22 = 0 |
i = 2, j = 3 aij = i - j a23 = 2 - 3 a23 = -1 |
|
i = 3, j = 1 aij = i - j a31 = 3 - 1 a31 = 2 |
i = 3, j = 2 aij = i - j a32 = 3 - 2 a32 = 1 |
i = 3, j = 3 aij = i - j a33 = 3 - 3 a33 = 0 |
So, the matrix A with order 3 x 3 is
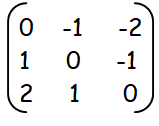
Now let us check whether it is symmetric or skew symmetric matrix.
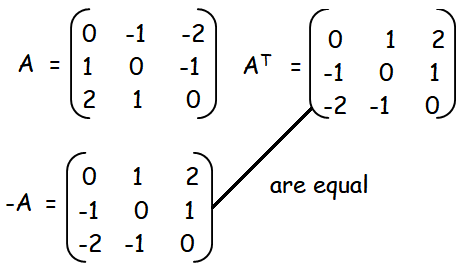
Hence it is skew symmetric matrix.
Question 2 :
Let A and B be two symmetric matrices. Prove that AB = BA if and only if AB is a symmetric matrix.
Solution :
If A and B are symmetric matrices, then
AT = A and BT = B
From the given question, we have to understand that we have to prove AB = BA if AB is symmetric matrix.
If AB is symmetric matrix, then we have to prove AB = BA. So, let us prove them as two cases.
Case 1 :
Prove that : AB = BA
Given : AB is symmetric
If AB is symmetric,
then (AB)T = AB
By using transpose law,
BTAT = AB
(BT = B and AT = A)
BA = AB
Hence proved.
Case 2 :
Prove that : AB is symmetric
Given : AB = BA
Let us take transpose for AB
(AB)T = BT AT
(AB)T = BA
From the given information, AB = BA.So let us replace BA as AB.
(AB)T = AB
Hence proved.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 5)
Jul 20, 24 01:23 AM
Digital SAT Math Problems and Solutions (Part - 5) -
SAT Math Videos - Part 9 (No Calculator)
Jul 19, 24 07:30 AM
SAT Math Videos - Part 9 (No Calculator) -
Solving Simple Equations Word Problems (Part - 1)
Jul 19, 24 05:35 AM
Solving Simple Equations Word Problems (Part - 1)
