MATRIX INTRODUCTION
A matrix is a rectangular array or arrangement of entries or elements displayed in rows and columns within a square bracket [ ] or parenthesis ( ).
Usually matrices are denoted by the capital letters like
A, B, C .....
|
|
In any matrix
- Horizontal arrangements are known as rows
- The vertical arrangements are known as columns
|
First row Second row |
Order of a matrix :
A matrix having m rows and n columns is called matrix of order m x n or simply m x n matrix . In general m x n has the following form
|
The order of a matrix or the size of a matrix is known as the number of rows
or the number of columns which are present in that matrix.
|
The order of above matrix is 2 x 4. Because in the above matrix there are two rows and four columns.
The element which occurs in a11 = 5
The element which occurs in a12 = -2
The element which occurs in a13 = 7
The element which occurs in a14 = 9
The element which occurs in a21 = 3
The element which occurs in a22 = 1
The element which occurs in a23 = 2
The element which occurs in a24 = -8
Minor of matrix :
Minor of a matrix may defined as follows.
Let |A| = |[aij]| be a determinant of order n.
The minor of an arbitrary element aij is the determinant obtained by deleting the ith row and jth column in which the element aij stands. The minor of aij by Mij.
Examples of finding minor of a matrix
Cofactor of matrix :
The cofactor is a signed minor. The cofactor of aij is denoted by Aij and is defined as Aij = -1(i+j) Mij.
|
Examples of finding cofactor of matrix
Adjoint of matrix :
Let A = [aij] be a square matrix of order n. Let Aij be a cofactor of aij. Then nth order matrix [Aij]T is called adjoint of A. It is denoted by adj A. In other words we can define adjoint of matrix as transpose of co factor matrix.
Examples of finding adjoint of matrix
Inverse of matrix :
If A is a non-singular matrix,there exists an inverse which is given by
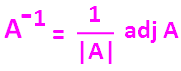
Examples of finding inverse of matrix
Related Pages
- Types of matrices
- Equality of matrices
- Operation on matrices
- Algebraic properties of matrices
- Multiplication properties
- Minor of a matrix
- Practice questions of minor of matrix
- Adjoint of matrix
- Adjoint of matrix worksheets
- Determinant of matrix
- Inverse of a matrix
- Practice questions of inverse of matrix
- Inversion method
- Inversion method worksheets
- Cramer's Rule for 3 equations
- Cramer's Rule for 2 equations
- Solving 2 equations using Cramer's method
- Rank Method in Matrix
- Rank of a matrix
- Solving using rank method
- Linear dependence of vectors
- Linear dependence of vectors in rank method
- Characteristic Equation of matrix
- Characteristic vector of matrix
- Diagonalization of matrix
- Gauss elimination method
- Matrix calculator
- Matrix worksheets
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Model Polynomial Multiplication
Oct 25, 20 05:39 AM
Model Polynomial Multiplication
-
Properties of Quadratic Equations
Oct 25, 20 03:45 AM
Properties of Quadratic Equations
-
Properties of Equality
Oct 25, 20 03:22 AM
Properties of Equality - Concept - Solved Problems
Featured Categories
2. Matrix Inverse Calculator - 2x2 Matrix
3. Matrix Inverse Calculator - 3x3 Matrix
4. Matrix Inverse Calculator - 4x4 Matrix
5. Cramer's Rule Calculator - 3x3 Matrix
6. Matrix Addition Calculator - 3x3 Matrix
7. Matrix Subtraction Calculator - 3x3 Matrix
8. Matrix Multiplication Calculator - 2x2 Matrix
9. Matrix Multiplication Calculator - 3x3 Matrix
10. Matrix Determinant Calculator - 3x3 & 2x2 Matrix
11. Matrix Addition Calculator - 2x2 Matrix
12. Matrix Subtraction Calculator- 2x2 Matrix
13. Matrix Addition Calculator - 4x4 Matrix
14. Matrix Subtraction Calculator- 4x4 Matrix
15. Matrix Multiplication Calculator - 4x4 Matrix