OPERATIONS ON MATRICES

We have the following operations on matrices.

(i) Multiplication of a matrix by a scalar.

(ii) Addition and subtraction of two matrices.

(iii) Multiplication of two matrices.

Multiplication of a Matrix by a Scalar

Let A be a matrix and k be a scalar. The, we can define a new matrix kA by multiplying each element of the matric A by k.

For instance, if

In particular, if k = -1, then we have

kA = -A

This -A is called negative of the matrix A. Don’t say -A as a negative matrix.

Addition and Subtraction of Two Matrices

If A and B are two matrices of the same order, then their sum denoted by A + B, is again a matrix of same order, obtained by adding the corresponding entries of A and B.

Similarly subtraction A - B is defined as

A - B = A + (-1)B

Example 1 :

Compute A + B and A - B, if

Solution :

By the definitions of addition and subtraction of matrices, we have

A + B :

A - B :

Example 2 :

Find the sum A + B + C if A, B and C are given by

Solution :

Example 3 :

Determine 3A + 4B - C if A, B, and C are given by

Solution :

Example 4 :

Simplify.

Solution :

Multiplication of Two Matrices

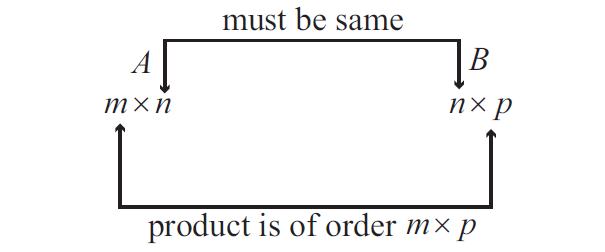
A matrix A is said to be conformable for multiplication with a matrix B if the number of columns of A is equal to the number of rows of B.

Let A be a matrix of order mxn and B be a matrix of order nxp.

Then the product of matrices A and B is denoted by AB  and its order is mxp.

The order of AB is

mxp = (number of rows of A) X (number of ncolumns of B)

For example, if A be a matrix of order 1x3 and B be a matrix of order 3x1, then AB is a matrix of order 1x1, that gives a element.

For instance,

Example 6 :

Find AB and BA if they exist, if

Solution :

The order of A is 3x3 and the order of B is 3x2.

Number of columns of A is 3 and number of rows of B is 3.

number of columns of A = number of rows of B

So, the product AB exists and the order of AB is 3x2.

The product BA does not exist, because

number of columns of A ≠ number of rows of B

Matrix Multiplication is Not Commutative

For two matrices A and B, even if AB and BA are defined, then AB = BA is not necessarily true. 

For instance, we consider

From (1) and (2) above,

AB ≠ BA

Properties of Matrix Addition and Scalar Multiplication

Let A, B, and C be three matrices of same order which are conformable for addition and a, b be two scalars. Then we have the following :

(1) A + B yields a matrix of the same order

(2) A + B = B + A (Matrix addition is commutative)

(3) (A + B) + C = A + (B + C) (Matrix addition is associative)

(4) A + O = O + A = A (O is additive identity)

(5) A + (-A) = O = (-A) + A (-A is the additive inverse of A)

(6) (a + b)A = aA + bA and a(A + B) = aA + aB

(7) a(bA) =(ab)A, 1A = A and 0A = O.

Properties of Matrix Multiplication

Using the algebraic properties of matrices we have,

(i) If A, B, and C are three matrices of orders mxn, nxp and pxq respectively, then A(BC) and (AB)C are matrices of same order mxq and 

A(BC) = (AB)C

(Matrix multiplication is associative)

(ii) If A, B, and C are three matrices of orders mxn, nxp, and nxp respectively, then A(B + C) and AB + AC are matrices of the same order mxp and

A(B + C) = AB + AC

(Matrix multiplication is left distributive over addition)

(iii) If A, B, and C are three matrices of orders mxn, mxn, and nxp respectively, then (A + B)C and AC + BC are matrices of the same order mxp and

(A + B)C = AC + BC

(Matrix multiplication is right distributive over addition)

(iv) If A, B are two matrices of orders mxn and nxp respectively and α is scalar, then

α(AB) = A(αB) = (αA)B

is a matrix of order mxp.

(v) If I is the unit matrix, then

AI = IA = A

(I is called multiplicative identity)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.