PRACTICE QUESTIONS ON PROPERTIES OF MATRICES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
If
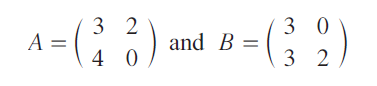
then find AB and BA. Are they equal ?
Question 2 :
If
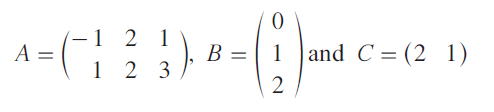
verify (AB)C = A(BC).
Question 3 :
If
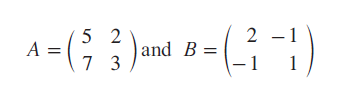
verify that (AB)T = BTAT
Question 4 :
Prove that
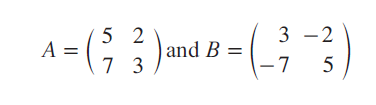
are inverse to each other under matrix multiplication.
Question 5 :
If
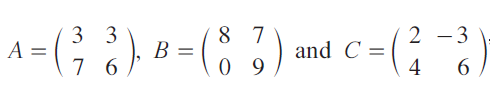
find (A + B)C and AC + BC. Is (A + B)C = AC + BC ?
Question 6 :
If A and B are square matrices such that
AB = I and BA = I
then B is
(A) Unit matrix
(B) Null matrix
(C) Multiplicative inverse matrix of A
(D) -A

Question 1 :
If
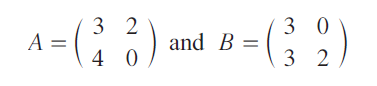
then find AB and BA. Are they equal ?
Solution :
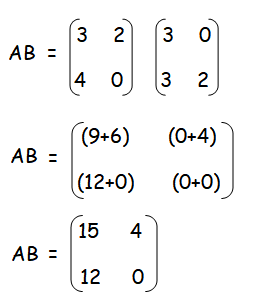
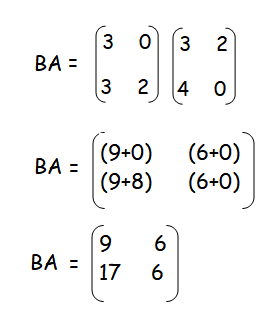
AB and BA are not equal.
Question 2 :
If
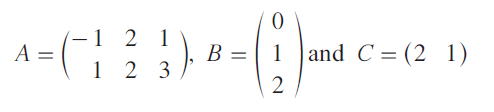
verify (AB)C = A(BC).
Solution :

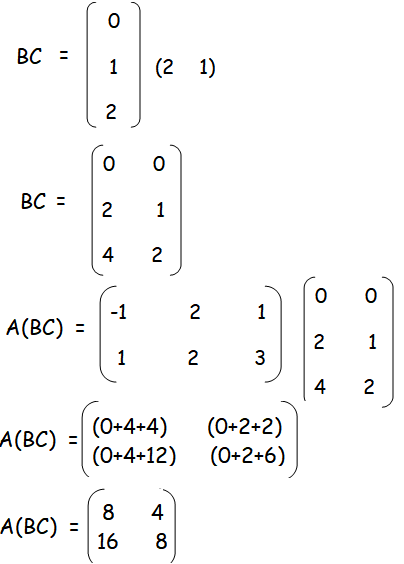
Associative property is true in matrix multiplication.
Question 3 :
If
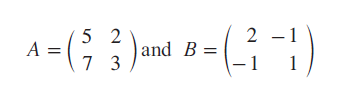
verify that (AB)T = BTAT
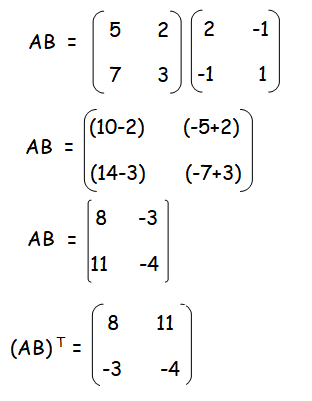
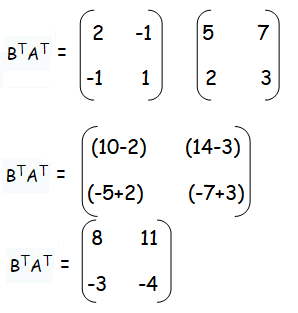
Question 4 :
Prove that
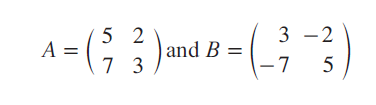
are inverse to each other under matrix multiplication.
Solution :
If A is a square matrix of order n, and if there exists a square matrix B of the same order n, such that
AB = BA = I
where I is the unit matrix of order n, then B is called the multiplicative inverse matrix of A.
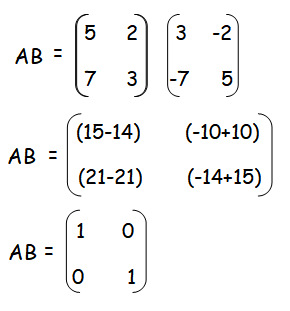
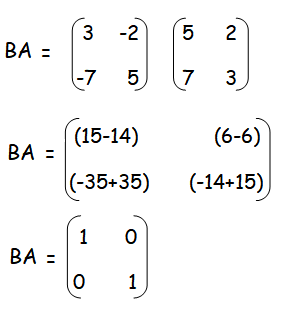
Question 5 :
If
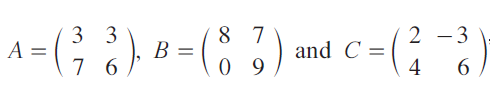
find (A + B)C and AC + BC. Is (A + B)C = AC + BC ?
Solution :
L.H.S :
Add matrices A and B, then multiply (A + B) by C.
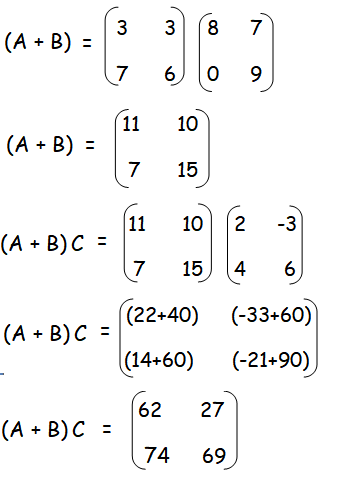
R.H.S :
Multiply the matrices A and C. Multiply the matrices B and C.
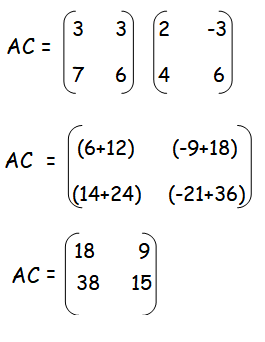
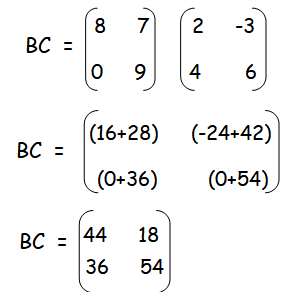
Add the matrices AC and BC.
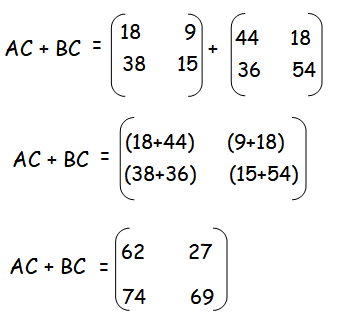
So, (A + B)C and AC + BC are equal.
Question 6 :
If A and B are square matrices such that
AB = I and BA = I
then B is
(A) Unit matrix
(B) Null matrix
(C) Multiplicative inverse matrix of A
(D) -A
Solution :
If A is a square matrix of order n, and if there exists a square matrix B of the same order n, such that
AB = BA = I
Then,
Matrices A and B are inverse to each other.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Tricky SAT Math Questions with Answers
Feb 25, 26 08:07 AM
10 Tricky SAT Math Questions with Answers -
Solving Exponential Equations
Feb 23, 26 10:06 AM
Solving Exponential Equations - Concept - Examples -
SAT Math Problems on Exponents and Radicals
Feb 21, 26 08:28 PM
SAT Math Problems on Exponents and Radicals
