Topics

                Math Formulas

Addition formula

Subtraction formula

Multiplication formula

Division formula

          Algebra

                Math Formulas

Formula for square

(a + b)² = a² + 2 ab + b²

(a - b)² = a² - 2 ab + b²

a² - b² = (a + b) (a - b)

a² + b² = (a + b)² - 2ab

a² + b² = (a - b)² + 2ab

a² + b² = ½ [(a + b)² - (a - b)²]

ab = ¼ [(a + b)² - (a - b)²]

(a - b)² = (a + b)² - 4 ab

(a + b)² = (a - b)² + 4 ab

(a+b+c)² =a²+b²+c²+2ab+2bc+2ca

(a-b+c)² =a²+b²+c²-2ab-2bc+2ca

(a-b-c)² =a²+b²+c²-2ab+2bc-2ca

Formula for cube

(a + b)³ = a³ + 3 a² b  + 3 a b² + b³

(a - b)³ = a³ - 3 a² b  + 3 a b² - b³

a³ + b³ = (a + b)³ - 3 ab (a + b)

a³ - b³ = (a - b)³ + 3 ab (a - b)

a³ + b³ = (a + b) (a² - ab + b²)

a³ - b³ = (a - b) (a² + ab + b²)

(x + a) (x + b) = x² + (a + b) x + ab

(x + a) (x + b) (x + c) =

x³+(a+b+c) x²+(ab+bc+ca) x+abc

a² + b² + c² - a b - b c - c a =

½[(a-b)²+(b-c)²+(c-a)²]

(a+b+c) (a² + b² + c² - a b-b c-c a) =

a³ + b³ + c³ - 3 a b c

          Logarithms

                Math Formulas

Product rule

log ₐ (m n) =  log ₐ m + log ₐ n

Quotient rule

log ₐ (m/n) =  log ₐ m - log ₐ n

Power rule

log ₐ m ⁿ = n log ₐ m

Change of base rule

log ᵤ m = (logᵥm) x (logᵤv)

Reciprocal rule

log ₐ i = 1/ logᵢ a

log ₐ 1 = 0

log ₐ a = 1

          Exponents

                Math Formulas

Product rule

Quotient rule

Power rule

Combination Law

Set theory

Math Formulas

Associative law

      A ∪ (B∪C)=(A∪B) U C

      A ∩ (B∩C)=(A∩B) ∩ C

Distributive law

    A ∪ (B∩C) = (A∪B) ∩ (A∪C)

    A ∩ (B∪C) = (A∩B) ∪ (A∩C)

De Morgan's law

      (i)(A∪B)'=A'∩B'.

      (ii)(A∩B)'=A'∪B'.

      (iii)A-(B∪C)=(A-B)∩(A-C)

      (iv)A-(B∩C)=(A-B)∪(A-C)

Cardinal number of power set

      n [p(A)] = 2 ⁿ

Identity laws

      A∪∅=A

      A∩U=U

Domination laws

      A∪U=U

      A∩∅=∅

Idempotent laws

      A∪A=A

      A∩A=A

Commutative laws

      A∪B=B∪A

      A∩B=B∩A

Sequence and series

Math Formulas

General form of an arithmetic progression 

a,(a+d),(a+2d),(a+3d),...........

a - first term d = common difference (t₂ - t₁)

nth term or general term of an A.P

Sum of n terms of an A.P

number of terms of an A.P

General form of g.p

a - first term r = common ratio (t₂/t₁)

Sum of n terms of g.p 

Trigonometry

Math Formulas

Trigonometric ratios

sin θ = Opposite side/Hypotenuse side

cos θ = Adjacent side/Hypotenuse side

tan θ = Opposite side/Adjacent side

Cosec θ = Hypotenuse side/Opposite side

Sec θ = Hypotenuse side/Adjacent side

cot θ = Adjacent side /Opposite side

Reciprocal

sin θ = 1/Cosec θ

Cosec θ = 1/sin θ

Cos θ = 1/sec θ

sec θ = 1/cos θ

tan θ = 1/cot θ

cot θ = 1/tan θ

identities

sin² θ  + cos² θ = 1

sin² θ  = 1 - cos² θ

cos² θ = 1 - sin² θ

Sec² θ - tan² θ = 1

Sec² θ  = 1 +  tan² θ

tan² θ  =  Sec² θ - 1

Cosec² θ - cot² θ = 1

Cosec² θ = 1 + cot² θ

cot² θ =  Cosec² θ - 1

Complementary angles

Sin (90 - θ) = cos θ

Cos (90 - θ) = sin θ

Tan (90 - θ) = cot θ

Cot (90 - θ) = tan θ

Cosec (90 - θ) = sec θ

Sec (90 - θ) = cosec θ 

Values of certain angles

Double angle formula

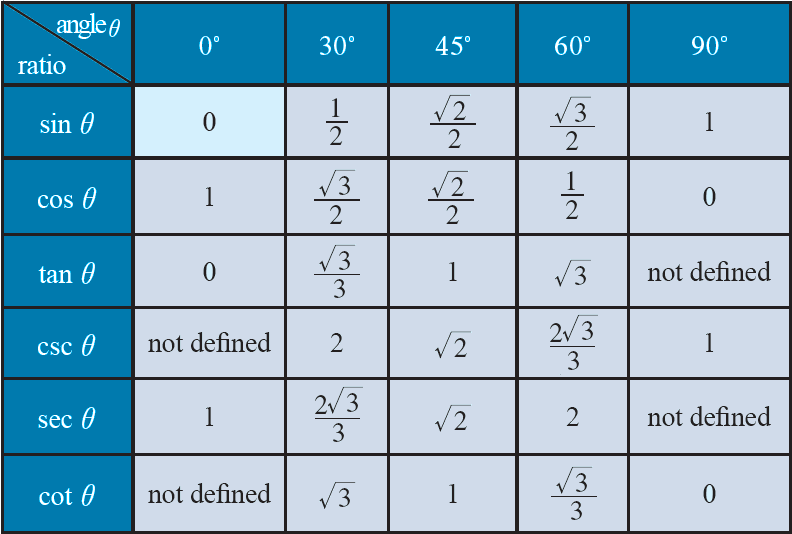Sin 2A = 2 Sin A cos A

Cos 2A = cos² A - Sin² A

tan 2A = 2 tan A/(1-tan² A)

Cos 2A = 1 - 2Sin² A

Cos 2A = 2Cos² A - 1

sin 2A = 2 tan A/(1+tan² A)

cos 2A = (1-tan² A)/(1+tan² A)

sin²A = (1-Cos 2A)/2

Cos²A = (1+Cos 2A)/2

Half angle formula

Sin A = 2 Sin (A/2) cos (A/2)

Cos A = cos² (A/2) - Sin² (A/2)

 tan A = 2 tan (A/2)/[1-tan² (A/2)]

Cos A = 1 - 2Sin² (A/2)

Cos A = 2Cos² (A/2) - 1

 sin A = 2 tan (A/2)/[1+tan² (A/2)]

cos A = [1-tan²(A/2)]/[1+tan² (A/2)]

 sin²A/2 = (1-Cos A)/2

Cos²A/2 = (1+Cos A)/2

 tan²(A/2) = (1-Cos A)/(1+Cos A)

Compound angle formula

Sin (A+B) = Sin A Cos B + Cos A Sin B

Sin (A-B) = Sin A Cos B - Cos A Sin B

Cos (A+B) = Cos A Cos B - Sin A Sin B

Cos (A-B) = Cos A Cos B + Sin A Sin B

tan (A+B) = [Tan A + Tan B] /(1- Tan A Tan B)

tan (A-B) = [Tan A - Tan B] /(1+ Tan A Tan B)

Compound angles sum and differences

sin(A+B)+Sin (A-B) = 2 Sin A cos B

sin(A+B)-Sin (A-B) = 2 Cos A sin B

cos(A+B)+Cos (A-B) = 2 Cos A cos B

cos(A+B)-Cos (A-B) = -2sin A sin B

3A formula

Sin 3A = 3 Sin A - 4 sin³A

Cos 3A = 4 Cos³A - 3 Cos A

tan 3A=(3 tan A - tan³A)/(1-3tan²A)

Sum to product formula

sin C + sin D = 2 sin [(C+D)/2] cos [(C-D)/2]

sin C - sin D = 2 cos [(C+D)/2] sin [(C-D)/2]

cos C + cos D = 2 cos [(C+D)/2] cos [(C-D)/2]

cos C - cos D = -2 sin [(C+D)/2] sin [(C-D)/2]

Analytical geometry

Math Formulas

Section formula internally

Section formula externally

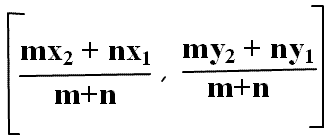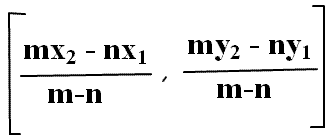Area of triangle using

Area of quadrilateral 

Centroid

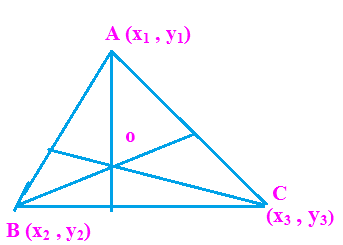(x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

Midpoint of the line segment

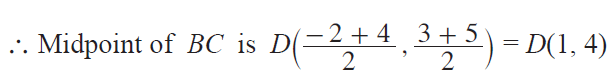(x₁ + x₂)/2 , (y₁ + y₂)/2

Distance between two points

√(x₂ - x₁) ² + (y₂ - y₁) ²

Slope of the line

m = tan θ

m = (y2 - y1)/(x2 - x1)

m = - coefficient of x / coefficient of y

y = m x + b

m-slope

Equation of the line

Slope intercept form:

y = m x + b

Here m = slope and b = y-intercept

Two point form:

(y-y₁)/(y₂-y₁) = (x-x₁)/(x₂-x₁)

Point- Slope form:

(y-y1) = m (x-x1)

Intercept form:

(X/a) + (Y/b) = 1

Perpendicular distance a point and a line

d=| (ax₁+by₁+c)/ va²+b²|

Angle between two lines

θ = tan-¹ |(m₁ - m₂)/(1 + m₁ m₂)|

Equation of circle

(x-h)² + (y-k)² = r² 

Equation of circle with two endpoints of diameter

(x-x₁) (x-x₂) + (y-y₁) (y-y₂) = 0

General equation of circle

x² + y² + 2gx + 2fy + c = 0

Length of the tangent

√ (x₁² + y₁² + 2gx₁ +2fy₁+c)

Condition of two circles touching externally

c₁c₂ = r₁ + r₂

Condition of two circles touching internally

 C₁ C₂ = r₁ - r₂

Orthogonal circles

2 g₁g₂+2f₁f₂=c₁+c₂

Differentiation

Math Formulas

d(xⁿ) =  n xⁿ⁻¹

d(sin x) = cos x

d(cos x)  - sin x

d(logₐ x) = 1/x log ₐ e

d(logₑ x) = 1/x

d(tan x) = sec² x

d(sec x)= sec x tan x

d(cot x)= - cosec²x

d(cosec x)= - cosec x cot x

d(Sin -¹ x)=  1/√(1-x²)

d(Cos -¹ x) = -1/√(1-x²)

d(tan -¹ x)= 1/(1+x²)

d(Cot -¹ x)= -1/(1+x²)

d(Sec -¹ x)=  1/[x√(x² - 1)]

d(cosec -¹ x)= -1/[x√(x² - 1)]

Product rule

(UV)' = UV' + VU'

Quotient rule

(U/V)' =  [VU' - UV'] /V²

Lagrange theorem

1.f(x) is defined and continuous on the closed interval [a,b] 

2.f(x) is differentiable on the open interval (a,b).

Then there exists at least one point c ∊ (a,b) such that 

f ' (c) = f (b) - f (a) / (b - a)

Rolle's theorem

1.f(x) is defined and continuous on the closed interval [a,b] 

2.f(x) is differentiable on the open interval (a,b).

3.f(A) = f(b)

then there exists at least one point c ∊ (a,b) such that f ' (c) = 0

Maclaurin series

Integration

Math Formulas

∫ xⁿ dx = x⁽ⁿ ⁺ ¹⁾/(n + 1) + c

∫ (1/xⁿ) dx = -1/(n - 1) x⁽ⁿ⁻¹⁾  + c

∫ (1/x) dx = log x  + c

∫ e^(x) dx = e^x  + c

∫ a^(x) dx = a^x/(log a)  + c

∫ Sin x dx = - Cos x + c

∫ Cos x dx = Sin x + c

∫ Cosec ² x dx = - Cot x  + c

∫ Sec ² x dx = tan x  + c

∫ sec x tan x dx = sec x  + c

∫ Cosec x cot x dx = - Cosec x  + c

∫ 1/(1 + x ²) dx =  tan ⁻ ¹x  + c

∫ 1/ √(1 - x ²) dx = Sin ⁻ ¹x   + c

∫ (ax + b)ⁿ dx = (1/a) (ax + b)⁽ⁿ ⁺ ¹⁾/(n + 1)   + c

∫ 1/(ax + b) dx = (1/a) log (ax + b) + c

∫ e^(ax + b) dx = (1/a) e^ (ax + b) + c

∫ Sin (ax + b) dx = -(1/a) Cos (ax + b) + c

∫ Cos (ax + b) dx = (1/a) Sin (ax + b) + c

∫ Sec ² (ax + b) dx = (1/a) tan (ax + b) + c

∫ Cosec ² (ax + b) dx = -(1/a) cot (ax + b) + c

∫ Cosec (ax+b)cot (ax+b)dx=-(1/a)Cosec (ax+b) + c

∫ sec (ax + b) tan (ax + b) dx = sec (ax + b) + c

∫ 1/1+ (ax) ² dx = (1/a) tan ⁻ ¹ (ax) + c

∫ 1/ √[1 - (ax ²)] dx = (1/a) Sin ⁻ ¹(ax)   + c

Integrating by parts

∫ u dv  = uv - ∫ v du

Mensuration

Formulas

Area of circle

Area of circle = Π r ²

Circumference of circle = 2 Π r

Area of triangle

Area of Equilateral-triangle = (√3/4) a²

Perimeter of Equilateral-triangle = 3a

Area of scalene triangle

Area of scalene triangle = √s(s-a)(s-b)(s-c)

Perimeter of scalene triangle

= a + b +  c

Area of semicircle

Area of Semi circle= (1/2) Π r²

Perimeter of semi-circle = Πr

Area of quadrant

Area of quadrant = (1/4) Π r²

Area of rectangle

Area of rectangle = L x W

Perimeter of rectangle=2(l+w)

Area of square

Area of square = a²

Perimeter of square = 4a

Area of parallelogram

Area of parallelogram = b x h

Area of quadrilateral

Area of quadrilateral

=(1/2) x d x (h₁+h₂)

Area of rhombus

Area of rhombus =(1/2) x (d₁ x d₂)

Area of trapezoid

Area of trapezoid =(1/2) (a + b) x h

Area of sector

Area of the sector = (θ/360) x Π r ² square units

(or)  Area of the sector = (1/2) x l r square units   

Length of arc = (θ/360) x 2Πr

Cylinder

Curved surface area = 2 Π r h

Total Curved surface area = 2 Π r (h+r)

Volume = Π r²h

Cone

Curved surface area = Π r l

Total Curved surface area = Π r (L+r)

Volume = (1/3)Π r²h

L² = r² + h²

sphere

Curved surface area = 4Π r²

Volume = (4/3)Π r³

Hemisphere

Curved surface area = 2Π r²

Total Curved surface area=3Π r²

Volume = (2/3)Π r³

Cuboid

Curved surface area=4h(l+b)

Total surface area = 2(lb+bh+h l)

Volume = l x b x h

Cube

Curved surface area=4a²

Total surface area = 6a²

Volume = a³