4th GRADE MATH QUIZ

Problem 1 :

Arrange the following digits so that they make smallest possible number.

8, 4, 5, 9, 7, 6, 1, 3, 2

 (A) 142356789           (B) 132456789       (C) 123456789

Solution :

The smallest possible number that can be formed by the given digits.

123456789

Problem 2 :

Write the number that is 1000 more than 636272

 (A) 637212         (B) 637272            (C) 632714

Solution : 

636272 + 1000  =  637272

Problem 3 :

Write the roman numeral for XXVIII

 (A) 42                (B) 28              (C) 36

Solution :

Roman numeral for XXVIII is 28.

Problem 4 :

Fill in the blank with the biggest digit possible.

764 _ 28.This number is divisible by 9. 

(A) 3                       (B) 9                     (C) 7

Solution :

Let x be the unknown

7 + 6 + 4 + x + 2 + 8  =  27 + x

If x is 9, we get 36 and it is divisible by 9.

So, the answer is 9.

Problem 5 :

A number which does not have a factor other than the number itself and 1, is called _______________ number.

 (A) Prime            (B) Composite        (C) None of these

Solution :

The number which does not have a factor other than 1 and itself is known as prime number.

Problem 6 :

The number which divides another number and gives no remainders is a ____________ of that number.

 (A) divisor              (B) factor          (C) none of these

Solution :

For example, let us divide 6 by 2. We get 3 as quotient and 0 as remainder.

So, 2 is the factor of 6.

Problem 7 :

Find the HCF of 96 and 120.

 (A) 24             (B) 35           (C) 12

Solution :

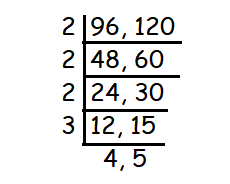
  =  2 ⋅ 2 ⋅ 2 ⋅ 3

  =  24

So, the highest common factor is 24.

Problem 8 :

Find the value of 56.725 + 48.258 - 32.564

 (A) 148.63           (B) 59.478        (C) 72.419

Solution :

56.725 + 48.258  ==>  104.983

104.983 - 32.564  ==>  72.419

Problem 9 :

In an Army camp provisions were there for 500 men for 28 days . If 400 men attended the camp, then how long did the provisions last ?

 (A) 35 days           (B) 10 days      (C) 50 days

Solution :

Number of men came to provision  =  550

Number of days did it run  =  28

Total contextion  =  550 ⋅ 28  =  15400

If, number of men have come to the provision  =  700

Then, number of days will it run  =  15400 / 700

  =  22 days.

If 700 men would have come, then the provision would have run for 22 days.

Problem 10 :

Find the number of days from November 10ᵗʰ 1997 to April 15ᵗʰ 1998.

 (A) 85 days             (B) 156 days      (C) 79 days

Solution :

November  =  31 - 10 ==>  21

December  =  30

January  =  31

February  =  28

March  =  31

April  =  15

  =  21+ 30 + 31 + 28 + 31 + 15

  =  156 days

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.