10 Hard SAT Math Questions (Part - 30)

Question 1 :

If k – x is a factor of –x² + (1/29)nk², where n and k are constants and k > 0, what is the value of n?

A) –29

B) – 1/29

C) 1/29

D) 29

Answer :

Question 2 :

In triangle ABC, sin ∠A = cos ∠B. If m∠A = (6y – 1)°, m∠B = (8y + 7)° and m∠C = (2x + y)°, what is the value of x?

Answer :

Question 3 :

John can complete a job in 20 minutes. Bob can complete the same job in 40 minutes. If they work together, approximately how many minutes will it take them to complete the job?

A) 60 minutes

B) 40 minutes

C) 30 minutes

D) 15 minutes

Answer :

Question 4 :

f(x) = –2x² + jx – 5

g(x) = 2x² + kx + 7

For the two functions above, f(x) has its maximum value and g(x) has its minimum value for the same value of x. What is the value of j + k?

Answer :

Question 5 :

Two spheres have radii in the ratio 12 : 13. The difference in their surface areas is 400π square inches. If the volume of the smaller sphere can be written as vπ, what is the value of v?

Answer :

Question 6 :

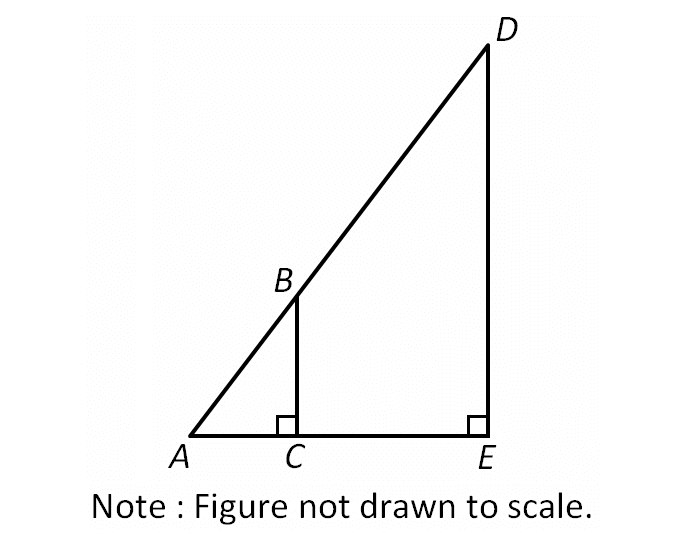
In the figure shown, AB = √185 units, AC = 4 units and CE = 10 units. What is the area, in square units, of triangle ADE?

Answer :

Question 7 :

The function q is defined by

q(x) = a|x – 9|² – 53|x – 9|+ b

where a and b are constants, and a > b > 53. If q(539) = h and q(–521) = k, where h and k are constants, what is the value of

32(–539)^h^{– k} + 347(9)^k^{– h} ?

Answer :

Question 8 :

A bird-watching group initially observed 200 birds in a certain area and set a goal of reaching 800 birds. According to their model, the population starts at 200 and increases by 30 birds per week for the first two weeks after the observation. After those two weeks, the population increases by 50 birds per week until the goal of 800 birds is reached. At the end of week w (where w > 2) after the initial observation, let p(w) be the predicted number of birds still needed to reach the 800-bird goal. Which of the following functions correctly represents p(w)?

A) p(w) = 800 – 50w

B) p(w) = 750 + 50w

C) p(w) = 640 – 50w

D) p(w) = 260 + 50w

Answer :

Question 9 :

A circle in the xy-plane has its center at (2, –3) and has a radius of 7. An equation of this circle is x² + y² + ax + by + c = 0, where a, b and c are constants. What is the value of c?

Answer :

Question 10 :

A circle has center G, and points M and N lie on the circle. Line segments MH and NH are tangent to the circle at points M and N, respectively. If the radius of the circle is 150 millimeters and the perimeter of quadrilateral GMHN is 3,500 millimeters, what is the distance, rounded to the nearest millimeter, between points G and H?

A) 150

B) 1,600

C) 1,607

D) 1,617

Answer :