X AND Y INTERCEPTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The x-intercept is the x-coordinate of the point where the graph intersects the x-axis. The y-coordinate of this point is always 0.
The y-intercept is the y-coordinate of the point where the graph intersects the y-axis. The x-coordinate of this point is always 0.
Finding Intercepts
Find the x- and y-intercepts.
Example 1 :
Solution :
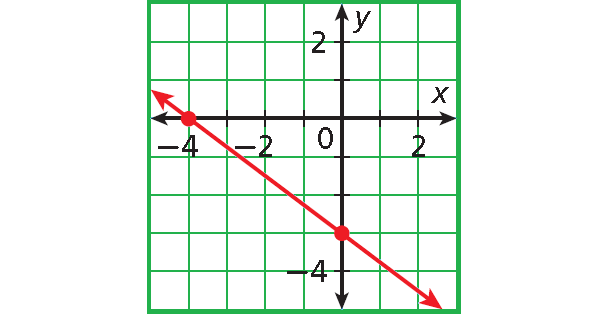
The graph intersects the x-axis at (-4, 0).
The x-intercept is -4.
The graph intersects the y-axis at (0, -3).
The y-intercept is -3.
Example 2 :
3x - 2y = 12
Solution :
To find the x-intercept, replace y with 0 and solve for x.
3x - 2y = 12
3x - 2(0) = 12
3x - 0 = 12
3x = 12
3x/3 = 12/3
x = 4
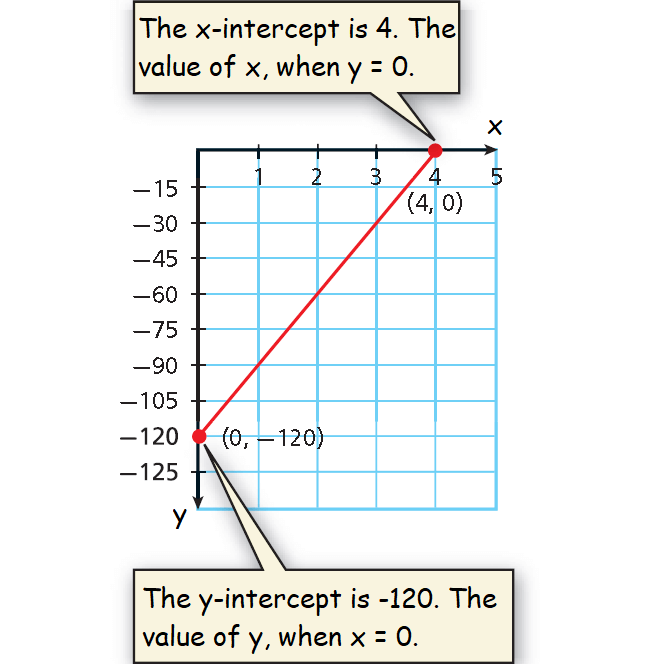
The x-intercept is 4.
To find the y-intercept, replace x with 0 and solve for y.
3x - 2y = 12
3(0) - 2y = 12
0 - 2y = 12
-2y = 12
-2y/(-2) = 12/(-2)
y = -6
The y-intercept is -6.
Travel Application
Example 3 :
A tramway travels a distance of about 4500 meters to the top of the peak. Its rate is 300 meters per minute. The function f(x) = 4500 - 350x gives the tram’s distance in meters from the top of the peak after x minutes. Graph this function and find the intercepts. What does each intercept represent?
Solution :
Neither time nor distance can be negative, so choose several nonnegative values for x. Use the function to generate ordered pairs.
|
x 0 5 10 15 |
f(x) = 4500 - 300x 4500 3000 1500 0 |
Graph the ordered pairs. Connect the points with a line.
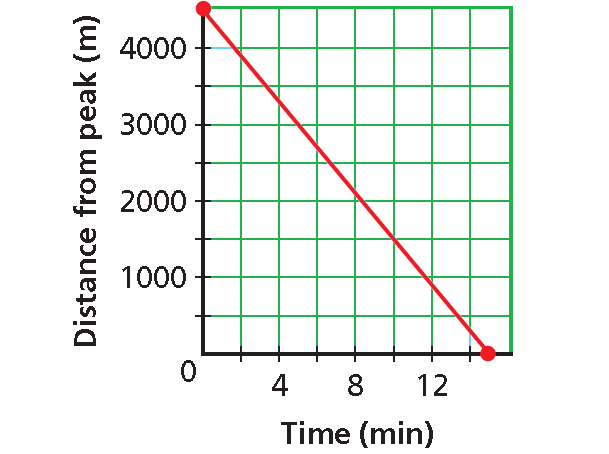
• y-intercept : 4500. This is the starting distance from the top (time = 0).
• x-intercept : 15. This the time when the tram reaches the peak (distance = 0).
Remember, to graph a linear function, you need to plot only two ordered pairs. It is often simplest to find the ordered pairs that contain the intercepts.
Graphing Linear Equations by Using Intercepts
Use intercepts to graph the line described by each equation.
Example 4 :
2x - 4y = 8
Solution :
Step 1 :
Find the intercepts.
x-intercept :
2x - 4y = 8
2x - 4(0) = 8
2x - 0 = 8
2x = 8
2x/2 = 8/2
x = 4
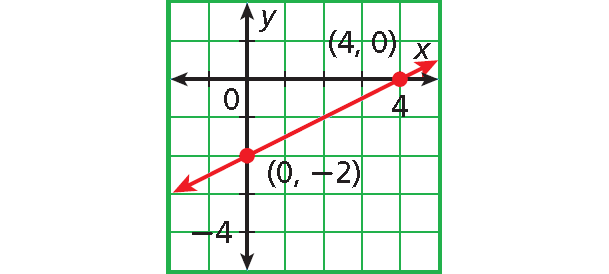
(4, 0)
y-intercept :
2x - 4y = 8
2(0) - 4y = 8
0 - 4y = 8
-4y = 8
-4y/(-4) = 8/(-4)
y = -2
(0, -2)
Step 2 :
Plot (4, 0) and (0, -2).
Connect with a straight line.
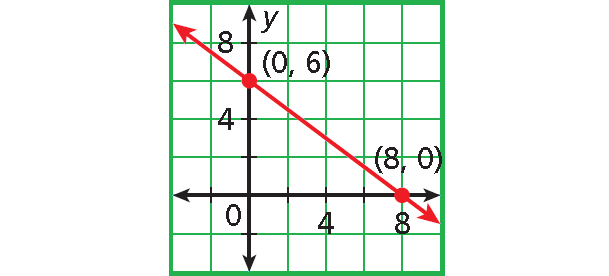
Example 5 :
2y = 12 - 3x/2
Solution :
Step 1 :
Write the equation in standard form.
2y = 12 - 3x/2
Multiply each side by 2.
4y = 24 - 3x
Add 3x to each side.
3x + 4y = 24
Step 2 :
Find the intercepts.
x-intercept :
3x + 4y = 24
3x + 4(0) = 24
3x + 0 = 24
3x = 24
3x/3 = 24/3
x = 8
(8, 0)
y-intercept :
3x + 4y = 24
3(0) + 4y = 24
0 + 4y = 24
4y = 24
4y/4 = 24/4
y = 6
(0, 6)
Step 3 :
Plot (8, 0) and (0, 6).
Connect with a straight line.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Simplifying Square Roots Worksheet
Feb 10, 26 07:29 AM
Simplifying Square Roots Worksheet -
Simplifying Square Roots
Feb 10, 26 07:26 AM
Simplifying Square Roots - Concept - Solved Questions -
GMAT Quantitative Reasoning Questions and Answers
Feb 10, 26 06:09 AM
GMAT Quantitative Reasoning Questions and Answers
