FINDING THE EQUATION OF A STRAIGHT LINE WORKSHEET

Question 1 :

Write the equations of the straight lines parallel to x- axis which are at a distance of 5 units from the x-axis.

Solution

Question 2 :

Find the equations of the straight lines parallel to the coordinate axes and passing through the point (-5, -2).

Solution

Question 3 :

Find the equation of a straight line whose

(i) slope is -3 and y-intercept is 4. 

(ii) angle of inclination is 60° and y-intercept is 3. 

Solution

Question 4 :

Find the equation of the line intersecting the y- axis at a distance of 3 units above the origin and tanθ = 1/2, where θ is the angle of inclination. 

Solution

Question 5 :

Find the equation of the straight line which passes through the midpoint of the line segment joining

(4, 2) and (3, 1)

whose angle of inclination is 30 degree.

Solution

Question 6 :

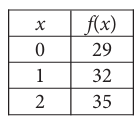
For the linear function f, the table shows three values of x and their corresponding values of f x equation defines f(x) ?

a)  f(x) = 3x + 29      b)  f(x) = 29x + 32

c)  f(x) = 35x + 29     d)  f(x) = 32x + 35

Solution

Question 7 :

Hana deposited a fixed amount into her bank account each month. The function

f(t) = 100t + 25

gives the amount, in dollars, in Hana’s bank account after t monthly deposits. What is the best interpretation of 25 in this context?

a) With each monthly deposit, the amount in Hana’s bank account increased by $25.

b) Before Hana made any monthly deposits, the amount in her bank account was $25.

c) After 1 monthly deposit, the amount in Hana’s bank account was $25.

d) Hana made a total of 25 monthly deposits.

Solution

Question 8 :

Which of the following equations represents a line that passes through (7, 6) and is parallel to the -x axis?

A) x = 6   B) x = 7    C) y = 6    D) y = 7

Solution

Question 9 :

Which of the following equations represents a line that passes through (-5, 1) and is parallel to the y axis?

A) y = -5   B) y = 1   C) x = -5    D) x = 1

Solution

Question 10 :

f(x) = ax + 2

In the function above, a is a constant. If f(-1) = 4, what is the value of f(-1/2) ?

Solution

Question 1 :

Find the slope and y-intercept of the line whose equation is y = x + 1.

Solution

Question 2 :

Find the slope and y-intercept of the line whose equation is 5x = 3y.

Solution

Question 3 :

Find the slope and y-intercept of the line whose equation is 4x - 2y + 1 = 0

Solution

Question 4 :

Find the slope and y-intercept of the line whose equation is 10x + 15y + 6 = 0.

Solution

Question 5 :

Find the equation of the straight line whose slope is -4 and passing through (1, 2).

Solution

Question 6 :

Find the equation of the straight line whose slope slope is 2/3 and passing through (5, -4).

Solution

Question 6 :

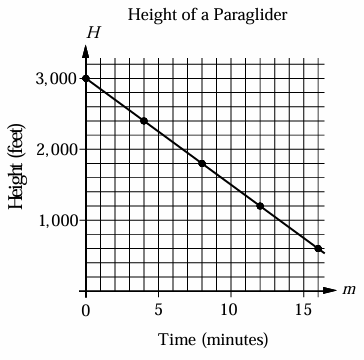
The graph above shows the relationship between the height of paraglider H, in feet, and time m, in minutes.

Which of the following represents the relationship between H and m? 

A) H(m) = -100m + 3000       B)  H(m) = -150m + 3000

C)  H(m) = -175m + 3000      D)   H(m) = -225m + 3000

Solution

Question 8 :

From the graph give above, if the height of the paraglider is 1,350 feet, which of the following best approximates the time the paraglider has been flying?

A) 10 minutes       B) 10 minutes and 30 seconds

C) 11 minutes        D) 11 minutes and 30 seconds

Solution

Question 9 :

A line in the xy plane passes through the point (1, -2) and has a slope of 1/3 .Which of the following points lies on the line?

A) (3, 2)      B) (2, -4/3)     C) (0, 2)      D) (-1, -8/3)

Solution

Question 10 :

If the slope of the line in the xy plane that passes through the points (2, -4) and (6, k) is 3/2 , what is the value of k?

Solution

Question 1 :

Find the equation of the straight line which passes through the midpoint of the line segment joining (4, 2) and (3, 1) whose angle of inclination is 30°.

Solution

Question 2 :

Find the equation of the straight line passing through the points

(-2, 5) and (3, 6)

Solution

Question 3 :

Find the equation of the straight line passing through the points

(0, -6) and (-8, 2)

Solution

Question 4 :

The manager of an apartment building needs an electrician to repair the power generator for the building. The table below shows the fixed amount for a time service call and hourly charges for two different companies.

Which of the following equations gives the total cost, y, of repairing the power generator in terms of the total number of hours, x, from company A?

a)  y = 48x + 75    b)  y = 75x + 48      c)  y = 40x + 55

d)  y = 55x + 40

Solution

Question 5 :

If point E (5, h) is on the line that contains A(0, 1) and B(-2, -1), what is the value of h ?

a)  -1     b)  0     c)  1     d)  3   e)  6

Solution

Question 6 :

The graph below displays the total cost C, in dollars of renting a boat for h hours.

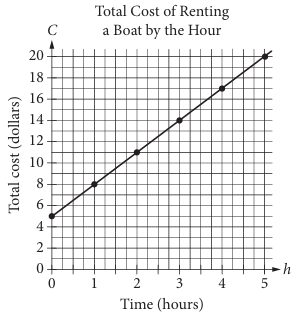
What does the C-intercept represent in the graph ?

a)  The initial cost of renting the boat

b)  The total number of boats rented

c)  The total number of hours the boat is rented.

d)  The increase in cost of rent the boat for each additional hour.

Solution

Question 7 :

Which of the following represents the relationship between h and C ?

a)  C = 5 h      b)  C = (3/4)h + 5   c)  C = 3h + 5    d) h = 3C

Solution

Question 8 :

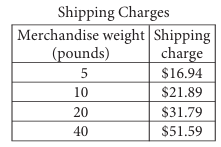
The table shows above shipping charges for an online retailer that sells sporting goods. There is a linear relationships between the shipping charge and the weight of merchandise. Which function can be used to determine the total shipping charge f(x), in dollars for an order with a merchandise weight of x pounds ?

a)  f(x) = 0.99x     b)  f(x) = 0.99x + 11.99

c)  f(x) = 3.39        d) f(x) = 3.39x + 16.94

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.