FINDING EQUATION OF THE LINE GIVEN TWO POINTS

Example 1 :

Find the equation of the straight line which passes through the midpoint of the line segment joining (4, 2) and (3, 1) whose angle of inclination is 30° .

Solution :

Let us draw a rough diagram based on the given information.

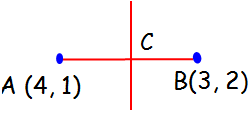
From the above diagram, we come to know that we have to find the line passing through the point C.

Midpoint of AB = (x₁ + x₂)/2, (y₁ + y₂)/2

A(4, 1) B(3, 2) 

  =  (4 + 3)/2 , (1 + 2)/2

  =  C (7/2, 3/2)

From the angle of inclination of the required line, we have to find the slope. 

m = tan θ  ==> tan 30° ==> 1/√3

Equation of the required line :

(y - y₂)  =  m(x - x₁)

(y - (3/2))  =  (1/√3) (x - (7/2))

√3 (y - (3/2))  =  1 (x - (7/2)) 

√3 (2y - 3)  =  1 (2x - 7) 

2√3 y - 3√3  =  2x - 7

2x - 2√3y - 7 + 3√3  =  0 

Hence equation of the required line is 2x - 2√3y + (3√3 - 7)  =  0

Example 2 :

Find the equation of the straight line passing through the points

(-2, 5) and (3, 6)

Solution :

Slope of the line joining these two points (-2, 5) and (3, 6)

m = (y₂ - y₁) / (x₂ - x₁)

= (6 - 5) / (3 + 2)

Slope = 1/5

Equation of the line :

(y - y₁) = m(x - x₁)

(y - 5) = (1/5)(x - (-2))

5(y - 5) = (x + 2)

5y - 25 = x + 2

x - 5y = -25 - 2

x-  5y = -27

Example 2 :

Find the equation of the straight line passing through the points

(0, -6) and (-8, 2)

Solution :

Slope of the line joining these two points (0, -6) and (-8, 2)

m = (y₂ - y₁) / (x₂ - x₁)

= (2 - (-6)) / (-8 - 0)

= (2 + 6) / (-8)

= -8/8

Slope = -1

Equation of the line :

(y - y₁) = m(x - x₁)

(y - (-6)) = -1(x - 0)

y + 6 = -x

x + y = -6

Example 3 :

The manager of an apartment building needs an electrician to repair the power generator for the building. The table below shows the fixed amount for a time service call and hourly charges for two different companies.

Which of the following equations gives the total cost, y, of repairing the power generator in terms of the total number of hours, x, from company A?

a)  y = 48x + 75    b)  y = 75x + 48      c)  y = 40x + 55

d)  y = 55x + 40

Solution :

Equation of linear function will be in the form 

y = mx + b

Company A :

Here m - slope = hourly rate = $55

y-intercept = fixed amount = $40

y = 55x + 40

So, option d is correct.

Example 4 :

If point E (5, h) is on the line that contains A(0, 1) and B(-2, -1), what is the value of h ?

a)  -1     b)  0     c)  1     d)  3   e)  6

Solution :

To find the value of h, we have to apply the point E in the equation of the line joining the points A and B.

Slope of line AB = (-1 - 1) / (-2 - 0)

= -2/(-2)

= 1

From the point A, when x = 0, y-intercept = 1

y = mx + b

y = 1x + 1

y = x + 1

Applying the point E(5, h), we get

h = 5 + 1

h = 6

So, option e is correct.

Example 5 :

The graph below displays the total cost C, in dollars of renting a boat for h hours.

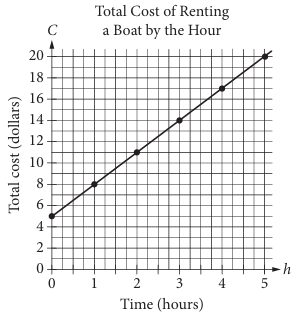
What does the C-intercept represent in the graph ?

a)  The initial cost of renting the boat

b)  The total number of boats rented

c)  The total number of hours the boat is rented.

d)  The increase in cost of rent the boat for each additional hour.

Solution :

x - number of hours

y - total cost

the initial cost of renting the boat.

Example 6 :

Which of the following represents the relationship between h and C ?

a)  C = 5 h      b)  C = (3/4)h + 5   c)  C = 3h + 5    d) h = 3C

Solution :

y-intercept = 5

Choosing two points on the line :

(1, 8) and (2, 11)

slope = (11 - 8) / (2 - 1)

= 3/1

= 3

C = 3h + 5

So, option c is correct.

Example 7 :

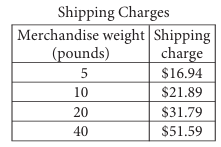
The table shows above shipping charges for an online retailer that sells sporting goods. There is a linear relationships between the shipping charge and the weight of merchandise. Which function can be used to determine the total shipping charge f(x), in dollars for an order with a merchandise weight of x pounds ?

a)  f(x) = 0.99x     b)  f(x) = 0.99x + 11.99

c)  f(x) = 3.39        d) f(x) = 3.39x + 16.94

Solution :

Choosing two points from the table,

(5, 16.94) and (10, 21.89)

Slope = (21.89 - 16.94) / (10 - 5)

= 4.95/5

= 0.99

Equation of line :

y = mx + b

y = 0.99x + b

The line passes through the point (5, 16.94)

16.94 = 0.99(5) + b

16.94 - 4.95 = b

b = 11.99

y = 0.99x + 11.99

So, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.