EXPLORING TRANSFORMATIONS OF PARENT FUNCTIONS

In this section, we will explore transformations of parent functions. 

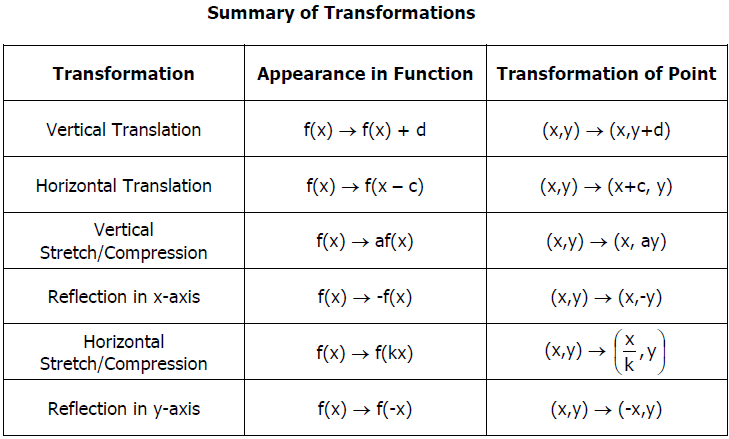
Transformations - Definition

A very simple definition for transformations is, whenever a figure is moved from one location to another location, a transformation occurs. 

If a figure is moved from one location another location, we say, it is transformation. Our next question is, how will the transformation be?. To know that, we have to be knowing the different types of transformations.

Now, let us come to know the different types of transformations.

Different Types of Transformations of Parent Functions

The different types of transformations which we can do in the parent functions are

1. Horizontal Translation

2. Vertical Translation

3. Reflection through the x-axis

4. Reflection through the y-axis

5. Horizontal Expansions and Compressions

6. Vertical Expansions and Compressions

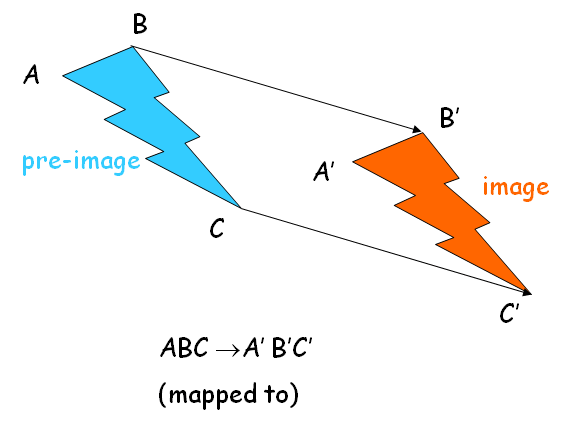
What is "Image" and "Pre-image"?

When a transformation occurs, the original figure is known as the pre-image and the new figure is known as the image.

It has been clearly shown in the below picture.

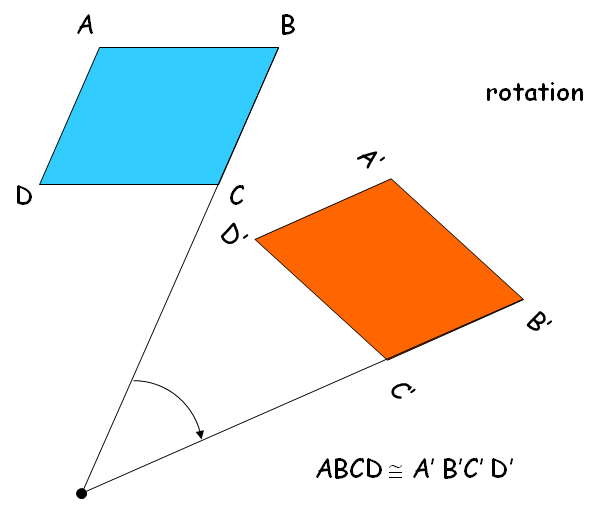
Rigid transformation or Isometry

A transformation where the pre-image and image are congruent is called a rigid transformation or an isometry.

It has been clearly shown in the below picture.

When a figure is moved from one location to another location, we say that it is a transformation.

In this point, always students have a question.

That is, if a figure is moved from one location to another location, we say, "it is transformation". How is this transformation made?

More clearly, on what grounds is the transformation made?

Is there any pre-decided rule to make transformation?

Yes, there is a pre-decided rule to make each and every transformation.

The rule we apply to make transformation is depending upon the kind of transformation we make.

We have already seen the different types of transformations in functions. 

For example, if we are going to make transformation of a function using reflection through the x-axis, there is a pre-decided rule for that. According to the rule, we have to make transformation.

The rule that we apply to make transformation using reflection and the rule we apply to make transformation using rotation are not same.

So, for each type of transformation, we may have to apply different rule.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.