REFLECTION ACROSS THE Y-AXIS

A reflection can be done across the y-axis by folding or  flipping an object over the y axis.

The original object is called the pre-image, and the reflection is called the image. If the pre-image is labeled as ABC, then the image is labeled using a prime symbol, such as A'B'C'.

An object and its reflection have the same shape and size, but the figures face in opposite directions. The objects appear as if they are mirror reflections, with right and left reversed.

Rule

Let y = f(x) be a function.

In the above function, if we want to do reflection across the y-axis, x has to be replaced by -x and we get the new function

y = f(-x)

The graph of y = f(-x) can be obtained by reflecting the graph of y = f(x) across the y-axis.

It can be done by using the rule given below.

That is, if each point of the pre-image is (x, y), then each point of the image after reflection over y-axis will be

(-x, y)

Example :

Do the following transformation to the function y = √x.

"A reflection across the y - axis"

And also write the formula that gives the requested transformation and draw the graph of both the given function and the transformed function

Solution :

Step 1 :

Since we do reflection transformation across the y-axis, we have to replace x by -x in the given function

y = √x

Step 2 :

So, the formula that gives the requested transformation is

y = √-x

Step 3 :

The graph y = √-x can be obtained by reflecting the graph of y = √x across the y-axis  using the rule given below.

(x, y) ----> (-x, y)

Step 4 :

The graph of the original function (given function)

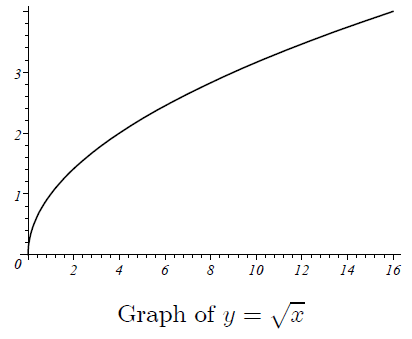
Step 5 :

The graph of the transformed function.

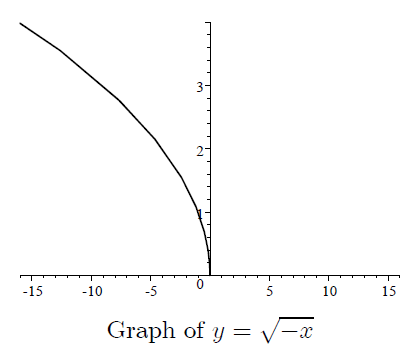
How to sketch the reflected graph across the y-axis?

In the above function, we can easily sketch the reflected graph across the y-axis.

For some other functions, students may find it difficult to sketch the reflected graph.

For example, students may find it difficult to sketch the reflected image of the triangle whose vertices are

A(-2, 1), B(2, 4) and C (4, 2)

To get the reflected image across the y-axis, they just have to apply the rule

(x, y) ----> (-x, y)

in the above three vertices.

When they do so, they can get the vertices of the reflected image.

They are

A'(2, 1) , B'(-2, 4) and C'(-4, 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.