VERTICAL TRANSLATIONS OF FUNCTIONS

Vertical translations of functions are the transformations that shifts the original graph of the function either up or down.

Definition

A vertical translation "slides" an object a fixed distance either up or down.  The original object and its translation have the same shape and size, and they face in the same direction.

In simple words, vertical translation means, it just moves the given figure either up or down  without rotating, re sizing or anything else.

Rule

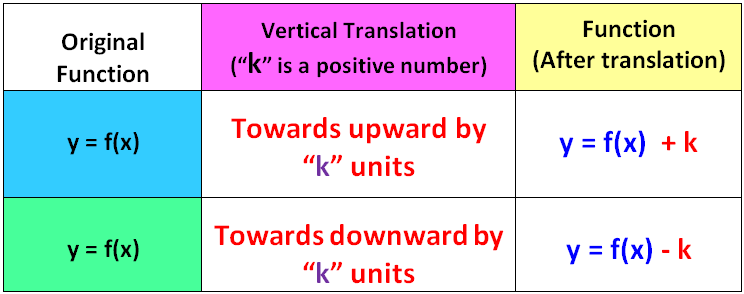
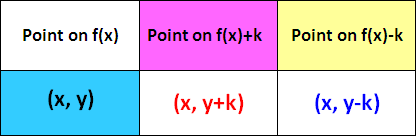
Let y = f(x) be a function and k be a positive number.

In the above function, if y is replaced by 'y - k, we get the new function

y - k = f(x)

or

y = f(x) + k

The graph of y = f(x) + k  can be obtained by  translating the graph  of y = f(x) towards upward by k units.

In case, y is replaced by y + k, we get the new function

y + k = f(x)

or

y = f(x) - k

The graph of y = f(x) - k can be obtained by translating the graph of y = f(x) towards downward by k units.

Moreover, if the the point  (x, y) is on the graph of

y = f(x),

then the point (x , y + k) is on the graph

y = f(x) + k

Example :

Perform the following transformation to the function

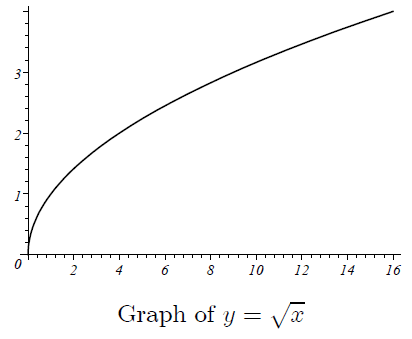
y = √x

"a translation upward by 3 units"

And also write the formula that gives the requested transformation and draw the graph of both the given function and the transformed function

Answer :

Step 1 :

Because we do a translation towards upward by 3 units, we have to replace y by y - 3 in the given function

y = √x 

Step 2 :

So, the formula that gives the requested transformation is

y - 3 = √x

or

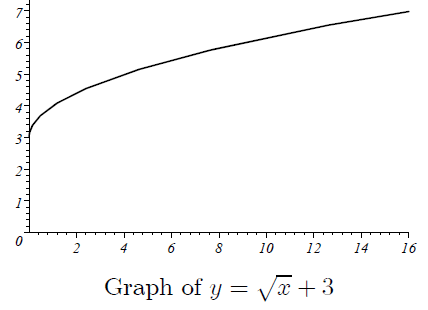
y = √x + 3

Step 3 :

The graph y = √x + 3 can be obtained by translating the graph of y = √x  toward upward by 3 units.

Step 4 :

The graph of the original function (given function).

Step 5 :

The graph of the transformed function.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.