ALGEBRAIC IDENTITIES
Algebraic identities are equalities which remain true regardless of the values of any variables which appear within it.
In our website, we have provided two calculators for algebraic identities.
One is to find the expansion for (a + b)n and other one is to find the expansion for (a - b)n.
Please click the below links to get the linear regression needed.
Expansion Calculator for (a + b)n
Expansion Calculator for (a - b)n
If you would like to have problems on algebraic identities, please click the link given below.
Worksheet on Algebraic Identities
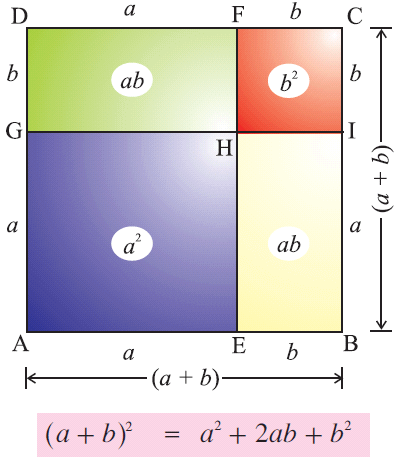
Proving Algebraic Identity Expansion Geometrically
In this section, we are going to see, how to prove the expansions of algebraic identities geometrically.
Let us consider algebraic identity and its expansion given below.
(a + b)2 = a2 + 2ab + b2
We can prove the the expansion of (a + b)2 using the area of a square as shown below.
Algebraic Identities Expansions
In this section, we are going to see the list of identities which are being used to solve all kind of problems in the Algebra.
|
(a + b)2 = a2 + 2ab + b2 (a + b)2 = (a - b)2 + 4ab | |
|
(a - b)2 = a2 - 2ab + b2 (a - b)2 = (a + b)2 - 4ab | |
|
a2 - b2 = (a + b)(a - b) | |
|
(x + a)(x + b) = x2 + (a + b)x + ab | |
|
(a + b)3 = a3 + 3a2b + 3ab2 + b3 (a + b)3 = a3 + 3ab(a + b) + b3 | |
|
(a - b)3 = a3 - 3a2b + 3ab2 - b3 (a - b)3 = a3 - 3ab(a - b) - b3 | |
|
a3 + b3 = (a + b)(a2 - ab + b2) a3 - b3 = (a - b)(a2 + ab + b2) | |
|
a3 + b3 = (a + b)3 - 3ab(a + b) a3 - b3 = (a - b)3 + 3ab(a - b) |
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
(a + b - c)2 = a2 + b2 + c2 + 2ab - 2bc - 2ac
(a - b + c)2 = a2 + b2 + c2 - 2ab - 2bc + 2ac
(a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ac
a2 + b2 = (a + b)2 - 2ab
a2 + b2 = (a - b)2 + 2ab
a2 + b2 = 1/2 ⋅ [(a + b)2 + (a - b)2]
ab = 1/4 ⋅ [(a + b)2 - (a - b)2]
(a + b + c)3 = a3 + b3 + c3 + 3a2b + 3a2c + 3ab2 + 3b2c + 3ac32 + 3bc2 + 6abc
(a + b - c)3 = a3 + b3 - c3 + 3a2b - 3a2c + 3ab2 - 3b2c + 3ac2 + 3bc2 - 6abc
(a - b + c)3 = a3 - b3 + c3 - 3a2b + 3a2c + 3ab2 + 3b2c + 3ac2 - 3bc2 - 6abc
(a - b - c)3 = a3 - b3 - c3 - 3a2b - 3a2c + 3ab2 - 3b2c + 3ac2 - 3bc2 + 6abc
How to remember algebraic identities with negative sign?
We can remember algebraic identities expansions like
(a + b)2, (a + b + c)2, (a + b + c)3
In the above identities, if one or more terms is negative, how can we remember the expansion ?
This question has been answered in the following three cases.
Case 1 :
For example, let us consider the identity of (a + b + c)2
We can easily remember the expansion of (a + b + c)2.
If c is negative, then we will have
(a + b - c)2
How can we remember the expansion of (a + b - c)2 ?
It is very simple.
Let us consider the expansion of (a + b + c)2.
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
In the terms of the expansion above, consider the terms in which we find "c".
They are c2, bc, ca.
Even if we take negative sign for "c" in c2, the sign of c2 will be positive. Because it has even power 2.
The terms bc, ca will be negative. Because both "b" and "a" are multiplied by "c" that is negative.
Finally, we have
(a + b - c)2 = a2 + b2 + c2 + 2ab - 2bc - 2ca
Case 2 :
In (a + b + c)2, if "b" is negative, then we will have
(a - b + c)2
How can we remember the expansion of (a - b + c)2 ?
It is very simple.
Let us consider the expansion of (a + b + c)2.
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
In the terms of the expansion above, consider the terms in which we find "b".
They are b2, ab, bc.
Even if we take negative sign for "b" in b2, the sign of b2 will be positive. Because it has even power 2.
The terms ab, bc will be negative. Because both "a" and "c" are multiplied by "b" that is negative.
Finally, we have
(a - b + c)2 = a2 + b2 + c2 - 2ab - 2bc + 2ca
Case 3 :
In (a + b + c)2, if both "b" and "c" are negative, then we will have
(a - b - c)2
How can we remember the expansion of (a - b - c)2 ?
It is very simple.
Let us consider the expansion of (a + b + c)2.
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
In the terms of the expansion above, consider the terms in which we find "b" and "c".
They are b2, c2, ab, bc, ac.
Even if we take negative sign for "b" in b2 and negative sign for "c" in c2, the sign of both b2 and c2 will be positive. Because they have even power 2.
The terms "ab" and "ca" will be negative.
Because, in "ab", "a" is multiplied by "b" that is negative.
Because, in "ca", "a" is multiplied by "c" that is negative.
The term "bc" will be positive.
Because, in "bc", both "b" and "c" are negative.
That is,
negative ⋅ negative = positive
Finally, we have
(a - b - c)2 = a2 + b2 + c2 - 2ab + 2bc - 2ca
In the same way, we can get idea to remember the the expansions of
(a + b - c)3, (a - b + c)3, (a - b - c)3
If you would like to have problems on algebraic identities, please click the link given below.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 161)
May 11, 25 12:34 AM
Digital SAT Math Problems and Solutions (Part - 161) -
Quadratic Equation Problems with Solutions (Part - 4)
May 10, 25 09:56 AM
Quadratic Equation Problems with Solutions (Part - 4) -
Digital SAT Math Problems and Solutions (Part - 160)
May 10, 25 12:14 AM
Digital SAT Math Problems and Solutions (Part - 160)