ALGEBRAIC IDENTITIES EXPANSIONS

Expansion Calculator for (a + b)ⁿ :

The calculator given in this section can be used to find the expansions of algebraic expressions in the form

(a + b)ⁿ

We can get the expansions of algebraic expressions in the above formula for any value of n.  

To get expansion calculator for (a - b)ⁿ,

Please click here

Proving Algebraic Identity Expansion Geometrically 

In this section, we are going to see, how to prove the expansions of algebraic identities geometrically. 

Let us consider algebraic identity and its expansion given below. 

(a + b)²  =  a² + 2ab + b² 

We can prove the the expansion of (a + b)² using the area of a square as shown below. 

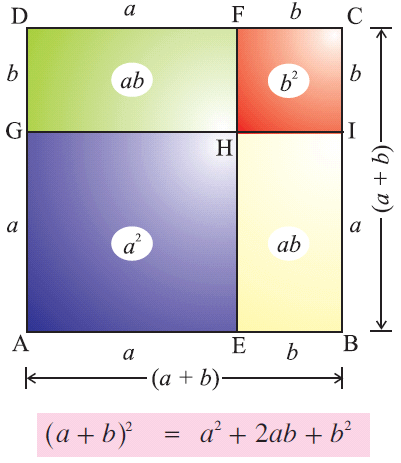
Algebraic Identities Expansions

a² + b²  =  (a + b)² - 2ab

a² + b²  =  (a - b)² + 2ab

(a + b + c)²  =  a² + b² + c² + 2ab + 2bc + 2ca

Square of Trinomials with Negative Sign

We have already the seen the expansion of (a + b + c)².

In (a + b + c)², if one or more terms is negative, how can we remember the expansion ?

This question has been answered in the following three cases. 

Case 1 :

For example, let us consider the identity of (a + b + c)²

We can easily remember the expansion of (a + b + c)². 

If 'c' is negative, then we will have 

(a + b - c)²

How can we remember the expansion of (a + b - c)² ?

It is very simple. 

Let us consider the expansion of (a + b + c)²_.

(a + b + c)²  =  a² + b² + c² + 2ab + 2bc + 2ca

In the terms of the expansion above, consider the terms in which we find 'c'.

They are c², bc, ca.

Even if we take negative sign for 'c' in c², the sign of c² will be positive.  Because it has even power 2. 

The terms bc, ca will be negative. Because both 'b' and 'a' are multiplied by 'c' that is negative.  

Finally, we have 

(a + b - c)²  =  a² + b² + c² + 2ab - 2bc - 2ca

Case 2 :

In (a + b + c)², if 'b' is negative, then we will have 

(a - b + c)²

How can we remember the expansion of (a - b + c)² ?

It is very simple. 

Let us consider the expansion of (a + b + c)²_.

(a + b + c)²  =  a² + b² + c² + 2ab + 2bc + 2ca

In the terms of the expansion above, consider the terms in which we find 'b'.

They are b², ab, bc.

Even if we take negative sign for 'b' in b², the sign of b² will be positive.  Because it has even power 2. 

The terms ab, bc will be negative. Because both 'a' and 'c' are multiplied by 'b' that is negative.  

Finally, we have 

(a - b + c)²  =  a² + b² + c² - 2ab - 2bc + 2ca

Case 3 :

In (a + b + c)², if both 'b' and 'c' are negative, then we will have

(a - b - c)²

How can we remember the expansion of (a - b - c)² ?

It is very simple. 

Let us consider the expansion of (a + b + c)²_.

(a + b + c)²  =  a² + b² + c² + 2ab + 2bc + 2ca

In the terms of the expansion above, consider the terms in which we find 'b' and 'c'.

They are b², c², ab, bc, ac.

Even if we take negative sign for 'b' in b² and negative sign for 'c' in c², the sign of both b² and c² will be positive.  Because they have even power 2. 

The terms 'ab' and 'ca' will be negative.

Because, in ab, 'a' is multiplied by 'b' that is negative. 

Because, in ca, 'a' is multiplied by 'c' that is negative.  

The term 'bc' will be positive.

Because, in 'bc', both 'b' and 'c' are negative.    

That is,

negative ⋅ negative  =  positive  

Finally, we have 

(a - b - c)²  =  a² + b² + c² - 2ab + 2bc - 2ca

In the same way, we can get idea to remember the the expansions of    

(a + b - c)³, (a - b + c)³, (a - b - c)³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.