ARITHMETIC SERIES PRACTICE WORKSHEET
Arithmetic Series Practice Worksheet :
This section will contain set of questions using the concept arithmetic series.
Arithmetic Series Practice Worksheet - Practice questions
(1) Find the sum of the following APs
(i) 2 , 7 , 12,....... to 10 terms Solution
(ii) -37, -33, -29,..................... to 12 terms Solution
(iii) 0.6, 1.7, 2.8,............... to 100 terms Solution
(iv) 1/15, 1/12, 1/10,................... to 11 terms Solution
(2) Find the sums given below
(i) 7 + 10 (1/2) + 14 + ...............+ 84 Solution
(ii) 34 + 32 + 30 + .................. + 10 Solution
(iii) - 5 + (-8) + (-11) + .............+ (-230) Solution
(3) In an AP
(i) Given a = 5, d = 3, an = 50 find n and Sn Solution
(ii) Given a = 7, a13 = 35 find d and S13 Solution
(iii) Given a12 = 37 , d = 3 find a and S12 Solution
(iv) Given a3 = 15 , S10 = 125 find d and a10 Solution
(v) Given d = 5 , S9 = 75 find a and a9 Solution
(vi) Given a = 2 , d = 8, Sn = 90 find n and an Solution
(vii) Given a = 8 , an = 62, Sn = 210 find n and d Solution
(viii) Given an = 4, d = 2, Sn = -14 find n and a Solution
(ix) Given a = 3, n = 8, Sn = 192 find d Solution
(x) Given l = 28 , S = 144 , and there are total 9 terms. Find a Solution
(4) How many terms of the AP 9, 17, 25,.......... must be taken to give a sum of 636? Solution
(5) The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and common difference. Solution
(6) The first and last term of an AP are 17 and 350 respectively.If the common difference is 9, how many terms are there and what is their sum? Solution
(7) Find the sum of first 22 terms of an AP in which d = 7 and 22nd term is 149. Solution
(8) The sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively. Solution
(9) If the sum of 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms. Solution
(10) Show that a₁,a₂,............ an form an AP where an is defined as below
(i) a n = 3 + 4 n Solution
(ii) a n = 9 - 5 n Solution
Also find the sum of 15 terms in each case.
(11) If the sum of the first n terms of an AP is 4 n - n² what is the first term (that is S)? what is the sum of first two terms?what is the second term? similarly find the 3rd,the 10th and the nth terms. Solution
(12) Find the sum of first 40 positive integers divisible by 6. Solution
(13) Find the sum of first 15 multiples of 8. Solution
(14) Find the sum of odd numbers between 0 and 50. Solution
(15) A contract on construction job specifies a penalty for delay for completion beyond a certain due date as follows. $200 for the first day, $250 for the second day, $300 for the third day etc., the penalty for each succeeding day being $50 more than for the preceding day. How much money the contractor has to pay as penalty,if he has delayed the work be 30 days. Solution
(16) A sum of $700 is to be used to seven cash prizes to students of a school for their overall academic performance. If each prize is $20 less than the preceding prize, find the value of each prizes. Solution
(17) In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in each they are studying ,e.g, a section of class I will plant 1 tree, a section of class II will plant 2 trees and so on till class XII. There are three sections of each class. How many trees will be planted by the students? Solution
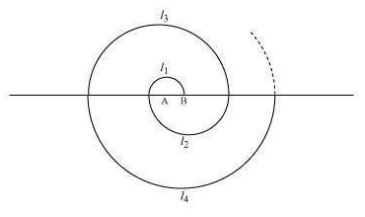
(18) A spiral is made up of successive semicircles,with centres alternately at A and B starting with center at A of radii 0.5, 1.0 cm, 1.5 cm ,2.0 cm ......... as shown in figure . What is the total length of spiral made up of thirteen consecutive semicircles. (∏ = 22/7) Solution

After having gone through the stuff given above, we hope that the students would have practiced questions in this worksheet.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems -
Factoring Trinomials Worksheet
Apr 25, 24 08:40 PM
Factoring Trinomials Worksheet
