WRITING COMPOUND INEQUALITIES FROM GRAPHS WORKSHEET

Write a compound inequality for each graph. 

1.

2.

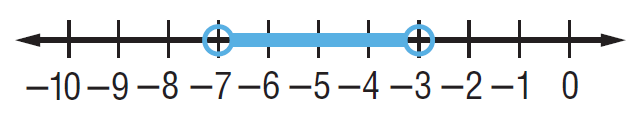
3.

4.

5.

6.

7.

One half a number increased by three is greater than 0 or less than or equal to -3.

8.  Describe and correct error in solving inequality or graphing the solution.

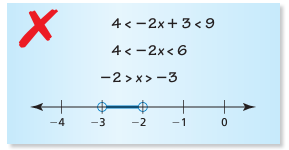
9.  Describe and correct error in solving inequality or graphing the solution.

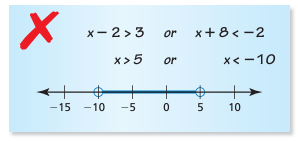
Detailed Solution

Problem 1 :

By observing the shaded region, the possible values of x are in between -2 and 2.

• Near -2 we have solid circle which means -2 should be included in the solution.
• Near 2, we have solid circle which means 2 also to be included.

Writing solution as inequality notation, we get

-2 ≤ x ≤ 2

Writing solution as interval notation, we get

[-2, 2]

Problem 2 :

By observing the shaded region, the possible values of x are in between -7 and 3.

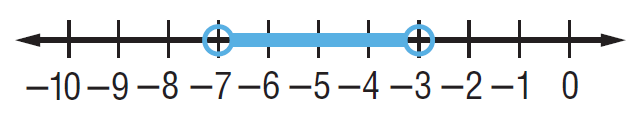
• Near -7 we have transparent circle which means -7 cannot be included in the solution.
• Near -3, we have transparent circle which means -3 cannot be included.

Writing solution as inequality notation, we get

-7 < x < -3

Writing solution as interval notation, we get

(-7, -3).

Problem 3 :

By observing the shaded portions, the possible values of x are lesser than or equal to 12 and greater than 15.

• At 12, we have solid circle. Which means 12 can be included. Lesser than or equal to 12. Then x ≤ 12
• At 15, we have transparent circle. Which means 15 should not be included. They are greater than 15. Then x ≤ 15

Writing solution as inequality notation, we get

-∞,< x < 12 or 15 < x < ∞

Writing solution as interval notation, we get

(-∞, 12] U (15, ∞)

Problem 4 :

By observing the shaded portions, the possible values of x are lesser than or equal to -7 and greater than -6.

• At -7, we have solid circle. Which means -7 can be included. Lesser than or equal to -7. Then x ≤ -7
• At -6, we have solid circle. Which means -6 should be included. They are greater than or equal to -6. Then x ≤ -6

Writing solution as inequality notation, we get

-∞ < x  ≤ -7 or -6  ≤ x < ∞

Writing solution as interval notation, we get

(-∞, -7] U [-6, ∞)

Problem 5 :

By observing the shaded portions, the possible values of x are lesser than or equal to -4 and x = 0

• At -4, we have solid circle. Which means -4 can be included. Lesser than or equal to -4. Then x ≤ -4
• At 0, we have solid circle. Which means 0 should be included. So, x = 0

Writing solution as inequality notation, we get

-∞ < x  ≤ -4 or x = 0

Writing solution as interval notation, we get

(-∞, -4] U x = 0

Problem 6 :

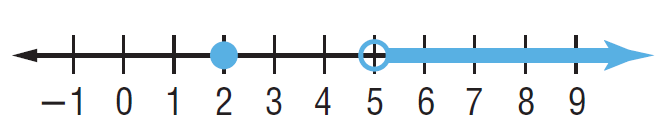
By observing the shaded portions, the possible values of x are greater than 5 and x = 2.

• At 2, we have solid circle. Which means 2 can be included. 
• At 5, we have transparent circle. Which means 5 should not be included. So, x > 5

Writing solution as inequality notation, we get

x = 2 or x>5

Writing solution as interval notation, we get

(5, ∞) U x = 2

Problem 7 :

One half a number increased by three is greater than 0 or less than or equal to -3.

Solution :

Let x be the number. Since it is one half of the number x/2.

• Increased by 3. Then (x/2) + 3 > 0
• Lesser than or equal to -3. Then x ≤ -3

Combining these two, we get

(x/2) + 3 > 0 (or) x ≤ -3

Problem 8 :

Describe and correct error in solving inequality or graphing the solution.

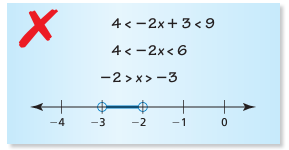
Solution :

4 < -2x + 3 < 9

Subtracting 3, we get

4 - 3 < -2x < 9 - 3

1 < -2x < 6

Dividing by -2, we get

-1/2 > x > -3

By reversing the inequality sign, we get

-3 < x < -1/2

So, there is a error.

Problem 9 :

Describe and correct error in solving inequality or graphing the solution.

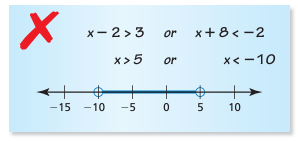
Solution :

x > 5 or x < -10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.