SOLVING EXPONENTIAL EQUATIONS

What is exponential equation?

It is an equation whose exponent or part of the exponent is a variable.

Examples :

3^x = 27

5^{3x - 1} = 625

Example 1 :

Solve for x :

3^x = 27

Solution :

3^x = 27

3^x = 3 ⋅ 3 ⋅ 3

3^x = 3³

Equate the exponents.

x = 3

Example 2 :

Solve for y :

Solution :

2^{y - 5} = 2^-4

Equate the exponents.

y - 5 = -4

Add 5 to both sides.

y = 1

Example 3 :

Solve for x :

6 ⋅ 3^x = 54

Solution :

7 ⋅ 3^x = 63

Divide both sides by 7.

3^x = 9

3^x = 3²

Equate the exponents.

x = 2

Example 4 :

Solve for z :

4^z = 7(2^z) + 18

Solution :

4^z = 7(2^z) + 18

(2²)^z = 7(2^z) + 18

(2^z)² = 7(2^z) + 18

(2^z)² - 7(2^z) - 18 = 0

Let a = 2^z.

a² - 7a - 18 = 0

(a - 9)(a + 2) = 0

a - 9 = 0  or  a + 2 = 0

In 3^z, whatever real value (positive or negative or zero) we substitute for z, 3^z can never be negative. So we can ignore the equation 3^z = -2.

Therefore,

z = 2

Example 5 :

Solve for t :

5^t = (√25)^-7 ⋅ (√5)^-5)

Solution :

5^t = (√25)^-7 ⋅ (√5)^-5

Equate the exponents.

t = -¹⁹⁄₂

Solving Exponential Equations Using Logarithms

Consider the following equation in exponential form.

b^y = a

The picture below illustrates how to convert the above equation from exponential to logarithmic form.

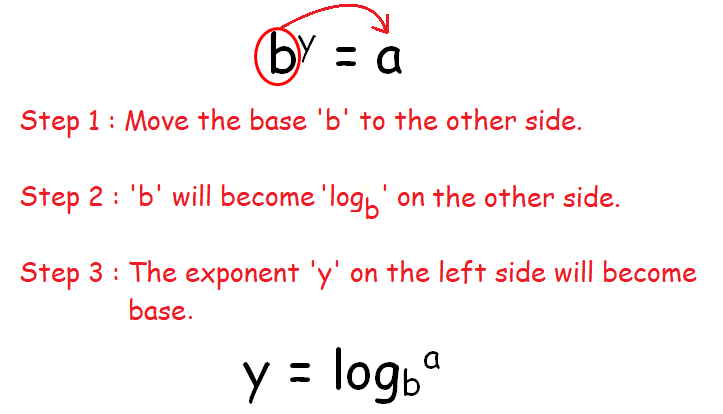
Still don't understand what is explained above, please watch the video below for step by step live explanation.

Example 6 :

Find the value of x, if 10^x = 100.

Solution :

10^x = 100

The above equation is in exponential form. Convert it to logarithmic form to solve for x.

x = log₁₀100

x = log₁₀100

x = log₁₀(10²)

x = 2log₁₀10

x = 2(1)

x = 2

Example 7 :

Find the value of x, if 3^x = ¹⁄₂₇.

Solution :

3^x = ¹⁄₂₇

The above equation is in exponential form. Convert it to logarithmic form to solve for x.

x = log₃(¹⁄₂₇)

x = log₃1 - log₃27

x = 0 - log₃(3³)

x = -3log₃3

x = -3(1)

x = -3

Example 8 :

Find the value of x, if 5^{3x - 1} = ¹⁄₆₂₅.

Solution :

5^{3x - 1} = ¹⁄₆₂₅

The above equation is in exponential form. Convert it to logarithmic form to solve for x.

3x - 1 = log₅(¹⁄₆₂₅)

3x - 1 = log₅1 - log₅625

3x - 1 = 0 - log₅(5⁴)

3x - 1 = -4log₅5

3x - 1 = -4(1)

3x - 1 = -4

Add 1 to both sides.

3x = -3

Divide both sides by 3.

x = -1

Example 9 :

Solve for x :

2^x - 1 = 5

Solution :

2^x - 1 = 5

Add 1 to both sides.

2^x = 5

On the left side of the equation above, the base is 2. On the right side, 6 is not a power of 2. So, we can not get the same base on both sides.

Take logarithm on both sides and solve for x.

log(2^x) = log6

Using power rule of logarithm,

xlog2 = log6

Divide both sides by log2.

Example 10 :

Solve for x :

5^{x - 1} - 2^x = 0

Solution :

5^{x - 1} - 2^x = 0

Add 2^x to both sides.

5^{x - 1} = 2^x

In the equation above, the base on the right side and the base left side are not same. And also, we can not make the base same on both sides using the rules of exponents.

Take logarithm on both sides and solve for x.

log(5^{x - 1}) = log(2^x)

Using power rule of logarithm,

(x - 1)log5 = xlog2

Using distributive property,

xlog5 - log5 = xlog2

Subtract xlog2 from both sides.

xlog5 - log5 - xlog2 = 0

Add log5 to both sides.

xlog5 - xlog2 = log5

Factor.

x(log5 - log)2 = log5

Divide both sides by (log5 - log2).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.