OPERATIONS ON MATRICES WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Add the following matrices.
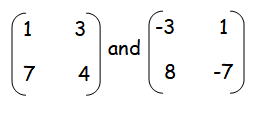
Question 2 :
Find the sum of the following matrices
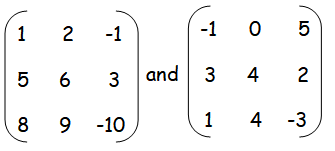
Question 3 :
Subtract the following matrices.
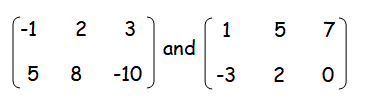
Question 4 :
Suppose the sum A+B+C exists. We also know that has 2 rows and C has 3 columns. What can we say about matrix B ?
Question 5 :
Given that
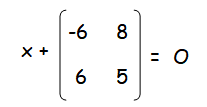
Where O is the 2x2 zero matrix, find the value of x.
Question 6 :
Given that
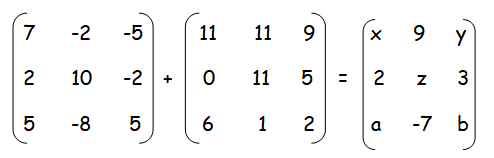
find the values of x, y, z, a and b.
Question 7 :
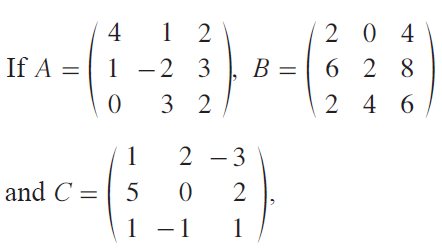
then, verify that A + (B + C) = (A + B) + C
Question 8 :
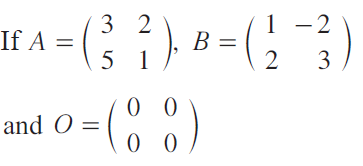
then verify:
(i) A + B = B + A
(ii) A + (- A) = O = (- A) + A
Question 9 :
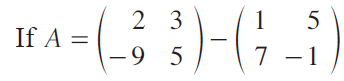
then find the additive inverse of A.
Question 10 :
If
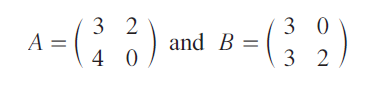
then find AB and BA. Are they equal ?
Question 11 :
If
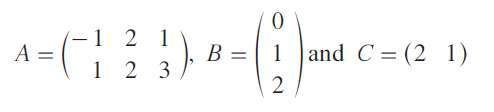
verify (AB)C = A(BC).
Question 12 :
If
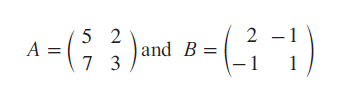
verify that (AB)T = BTAT
Question 13 :
Prove that
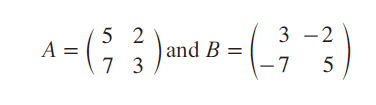
are inverse to each other under matrix multiplication.
Question 14 :
If
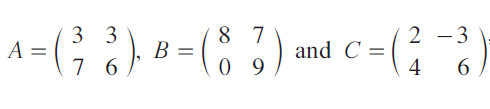
find (A + B)C and AC + BC. Is (A + B)C = AC + BC ?
Question 15 :
If A and B are square matrices such that
AB = I and BA = I
then B is
(A) Unit matrix
(B) Null matrix
(C) Multiplicative inverse matrix of A
(D) -A
Question 16 :
Find the values of x, y and z from the matrix equation
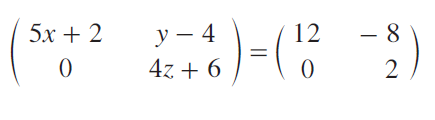
Question 17 :
Let
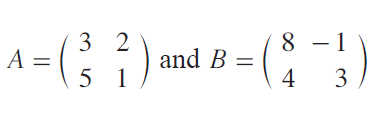
Find the matrix C if C = 2A + B
Question 18 :
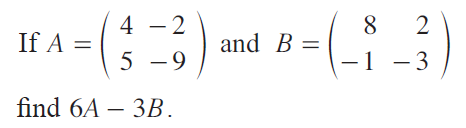
Question 19 :
Verify the property A(B + C) = AB + AC, when the matrices A, B, and C are given by
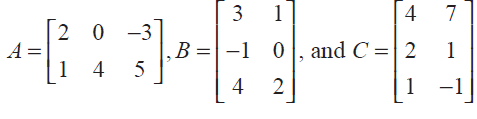
Question 20 :
Find the matrix A which satisfies the matrix relation
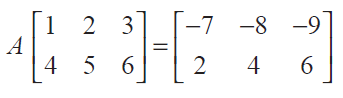
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Quantitative Reasoning Questions and Answers
Dec 14, 25 06:42 AM
Quantitative Reasoning Questions and Answers -
Specifying Units of Measure
Dec 14, 25 06:38 AM
Specifying Units of Measure -
Coin Tossing Probability
Dec 13, 25 10:11 AM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems