PRACTICE QUESTIONS ON PROPERTIES OF MATRICES

Question 1 :

If

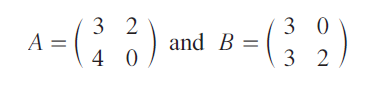
then find AB and BA. Are they equal ?

Question 2 :

If

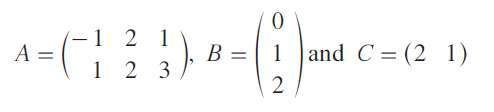
verify (AB)C  =  A(BC).

Question 3 :

If

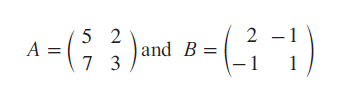
verify that (AB)^T  =  B^TA^T    

Question 4 :

Prove that

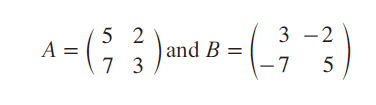
are inverse to each other under matrix multiplication.

Question 5 :

If

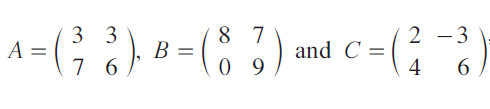
find (A + B)C and AC + BC. Is (A + B)C  =  AC + BC ?

Question 6 :

If A and B are square matrices such that

AB = I and BA = I 

then B is 

(A) Unit matrix

(B) Null matrix

(C) Multiplicative inverse matrix of A

(D) -A

Question 1 :

If

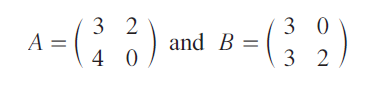
then find AB and BA. Are they equal ?

Solution :

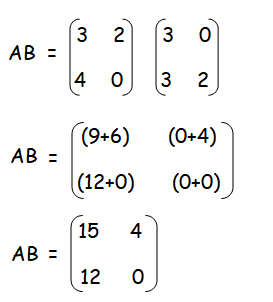
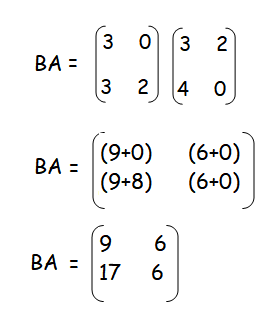
AB and BA are not equal.

Question 2 :

If

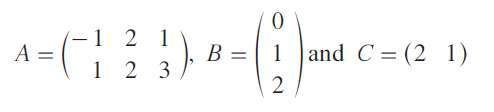
verify (AB)C  =  A(BC).

Solution :

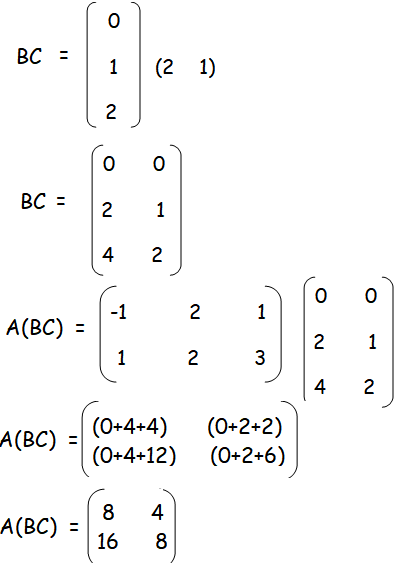
Associative property is true in matrix multiplication.

Question 3 :

If

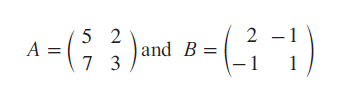
verify that (AB)^T  =  B^TA^T    

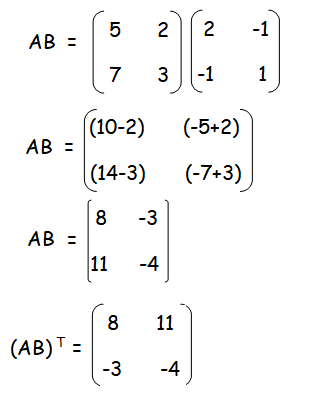
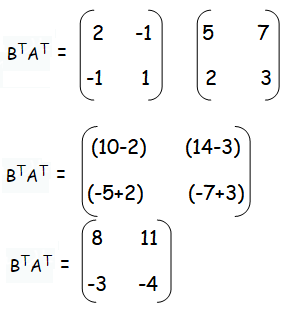
Question 4 :

Prove that

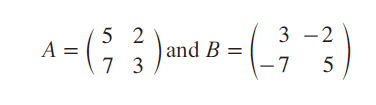
are inverse to each other under matrix multiplication.

Solution :

If A is a square matrix of order n, and if there exists a square matrix B of the same order n, such that

AB  =  BA  =  I

where I is the unit matrix of order n, then B is called the multiplicative inverse matrix of A.

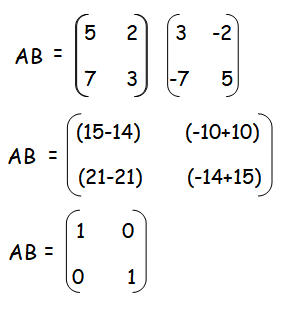
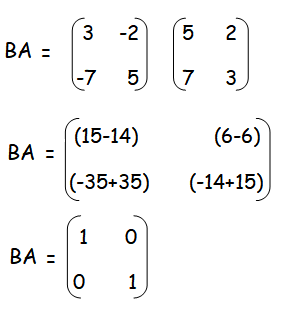
Question 5 :

If

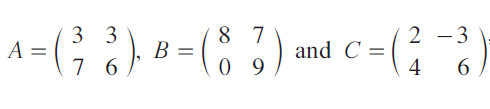
find (A + B)C and AC + BC. Is (A + B)C  =  AC + BC ?

Solution :

L.H.S :

Add matrices A and B, then multiply (A + B) by C.

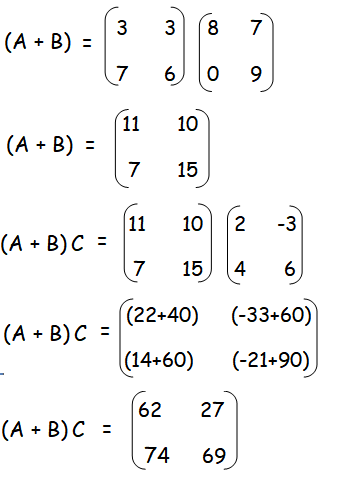
R.H.S :

Multiply the matrices A and C. Multiply the matrices B and C.

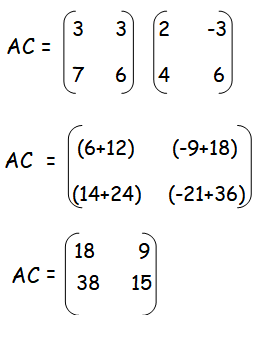
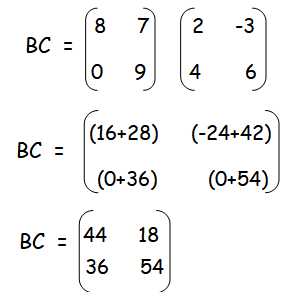
Add the matrices AC and BC.

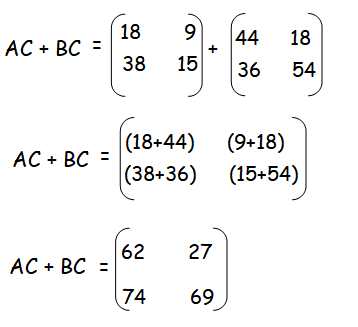
So,  (A + B)C and AC + BC are equal. 

Question 6 :

If A and B are square matrices such that

AB = I and BA = I 

then B is 

(A) Unit matrix

(B) Null matrix

(C) Multiplicative inverse matrix of A

(D) -A

Solution :

If A is a square matrix of order n, and if there exists a square matrix B of the same order n, such that

AB  =  BA  =  I

Then, 

Matrices A and B are inverse to each other.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.