VOLUME AND CAPACITY WORD PROBLEMS

The units for capacity and the units for volume are closely related.

1 mL of fluid will fill a cube 1 cm x 1 cm x 1 cm.

1 cm³ has capacity 1 mL

1 L of fluid will fill a cube 10 cm x 10 cm x 10 cm.

1000 cm³ has capacity 1 L

1 kL of fluid will fill a cube 1 m x 1 m x 1 m.

1 m³ has capacity 1 kL.

Example 1 :

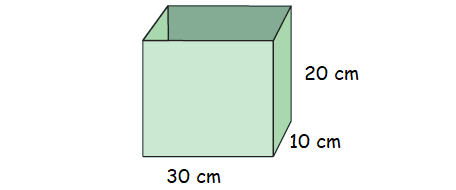
Calculate the capacity of the container:

Solution :

Volume of the container = 30 x 10 x 20 cm³

= 6000 cm³ 

1 cm³ = 1 mL

= 6000 mL

1000 ml = 1 L

= (6000/1000) L

= 6 L

So, the capacity of the container is 6 L.

Example 2 :

Find the capacity in liters of a fish tank 2 m by 1 m and 50 cm.

Solution :

Volume of tank = l x w x h

Substitute l = 2, w = 1 and h = 50 cm or 0.5 m.

= 2 x 1 x 0.50

= 1 m³

1 m³ = 1 KL

So, capacity of the tank is 1 KL.

Example 3 :

A rectangular petrol tank has dimensions 50 cm by 40 cm by 25 cm. How many liters of petrol are needed to fill it?

Solution :

Volume of rectangular tank  =  l x w x h.

Substitute l = 50, w = 40 and h = 25.

= 50 x 40 x 25

= 50000 cm³

1000 cm³ = 1 L

= 50000/1000

= 50 L

So, the capacity of the petrol tank is 50 L.

Example 4 :

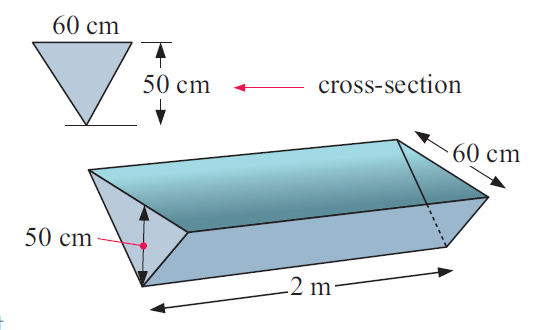
A water trough has triangular cross-section as shown. Its length is 2 m.

Find:

a) the area of the triangle in cm²

b) the volume of space in the trough in cm³

c) the capacity of the trough in :

i) litres   ii) kilolitres.

Solution :

Area of triangle :

= (1/2) ⋅ base ⋅ height

Base = 60 cm and height  =  50 cm

= (1/2) ⋅ 60 ⋅ 50

= 1500 cm³

Volume of space :

= (1/2) ⋅ Base area x height

= (1/2) ⋅ 1500 ⋅ 200

= 300000 cm³

1000 cm³ = 1 L

Capacity :

= 300000/1000

= 300 Liter

So, capacity of triangular prism is 300 liter.

1m³ = 1 KL

1000 ml = 1 kl

= 300/1000

= 0.3 kl

So, capacity of triangular prism is 0.3 kl.

Example 5 :

Find the capacity in megaliters of a reservoir with a surface area of 1 hectare and an average depth of 2.5 meters.

Solution :

1 hectare = 10000 m²

Volume = Surface area x height

= 10000 x 2.5

= 25000 m³

1 m³ = 1 KL

= 25000 KL

Capacity = 25000/1000 ML

= 25 ML

So, the capacity is 25 ML.

Example 6 :

A kidney-shaped swimming pool has surface area 15 m² and a constant depth of 2 meters. Find the capacity of the pool in kiloliters.

Solution :

Volume = Surface area x height

Surface area = 15 m² and height = 2 m

= 15 x 2

= 30 m³

1 m³ = 1 KL

= 30 KL

So, the capacity is 30 KL.

Example 7 :

A lake has an average depth of 6 m and a surface area of 35 ha. Find its capacity in megaliters.

Solution :

1 hectare = 10000 m²

35 hectare = 350000 m²

Height = 6 m

Volume = Surface area x height

= 350000 x 6

= 2100000 m³

1 m³ = 1 KL

= 2100000 Kl

1 ML = 1000 KL

= 2100000/1000 ML

= 2100 ML

So, the capacity of the tank is 2100 ML.

Example 7 :

A school provides milk to the students daily in a cylindrical glasses of diameter 7 cm. If the glass is filled with milk up to height of 12 cm, find how many litres of milk is needed to serve 1600 students.

Solution :

Radius = 7/2 ==> 3.5 cm

Height = 12 cm

Quantity of milk in the glass = πr²h

= 3.14 x 3.5² x 12

= 461.58 cm³

1000 cm³ = 1 liter

1 cm³ = 0.001 liter

461.58 cm³ = 461.58 x 0.001 liter

= 0.46158 liter

Quantity of milk to serve for 1600 students

= 0.46158 x 1600

= 738.528 liter

Approximately 739 liters.

Example 8 :

If the capacity of a cylindrical tank is 1848 m³ and the diameter of its base is 14 m. Find the depth of the tank.

Solution :

Capacity of the tank = 1848 m³

πr²h = 1848 m³

Here, radius = 14/2 ==> 7 m

3.14 x 7² x h = 1848

h = 1848/(3.14 x 49)

h = 12 m

So, the depthe of the tank is 12 m.

Example 8 :

A rectangular examination hall having seats for 500 candidates has to be built so as to allow 4 cubic metres of air and 0.5 square metres of floor area per candidate. If the length of hall be 25 m, find the height and breadth of the hall.

Solution :

Floor area per candidate = 0.5 square meter

length x width = 0.5

25 x width = 0.5

width = 0.5/25

= 0.02 m

Space occupied for 500 candidates = 4 cubic meter

500 x length x width x height = 4

500 x 25 x 0.02 x height = 4

height = 4/(500 x 25 x 0.02)

= 0.016 m

So, the height of the hall is 0.016 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.