USE THE EUCLIDEAN ALGORITHM TO FIND GCD OF THE GIVEN POLYNOMIALS

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Step 1 :

First, divide f(x) by g(x) to obtain

f(x) = g(x)q(x)+ r(x)

where q(x) is the quotient and r(x) is remainder,

so, deg (g(x)) > deg (r(x))

If the remainder r(x) is 0, then g(x) is the GCD of f(x) and g(x).

Step 2 :

If the remainder r(x) is non-zero, divide g(x) by r(x) to obtain

g(x) = r(x) q(x)+ r₁(x)

where r₁(x) is the remainder.

So, deg r(x) > deg r₁(x)

If the remainder r₁(x) is 0, then r(x) is the required GCD.

Step 3 :

If r₁(x) is non-zero, then continue the process until we get zero as remainder.

The remainder in the last but one step is the GCD of f(x) and g(x).

We write GCD(f(x), g(x)) to denote the GCD of the polynomials f(x) and g(x).

Find the GCD of the following pairs of polynomials using division algorithm

(i) x³-9x²+23x-15 and 4x²-16x+12

(ii) 3x³+18x²+33x+18, 3x²+13x+10

(iii) 2x³+2x²+2x+2, 6x³+12x²+6x+12

(iv) x³-3x²+4x-12, x⁴+x³+4x²+4x

(i) Answer :

x³-9x²+23x-15 and 4x²-16x+12

Let f(x) = x³-9x²+23x-15 and

g(x) = 4x²-16x+12

g(x) = 4(x²-4x+3)

Here, deg(f(x)) > deg (g(x))

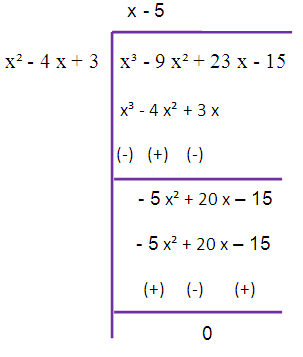
By dividing f(x) by g(x), we get 0 as remainder. So, the required GCD is x-5.

(ii) Answer :

3x³+18x²+33x+18, 3x²+13x+10

Let f(x) = 3x³+18x²+33x+18 and g(x) = 3x²+13x+10

Here, deg f(x) > deg g(x)

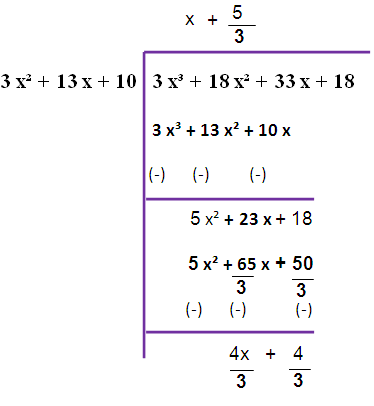
By dividing f(x) by g(x) we are not getting zero. So, we have to do this long division once again.

Now we are taking 4/3 as common from the remainder. So that we are getting (4/3)(x+1)

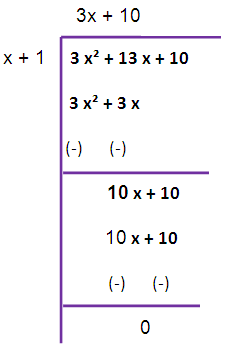
So, the greatest common divisor is x+1.

(iii) Answer :

2x³+2x²+2x+2, 6x³+12x²+6x+12

Let f(x) = 2x³+2x²+2x+2 and g(x) = 6x³+12x²+6x+12

f(x) = 2(x³+x²+x+1)

g(x) = 6(x³+2x²+x+2)

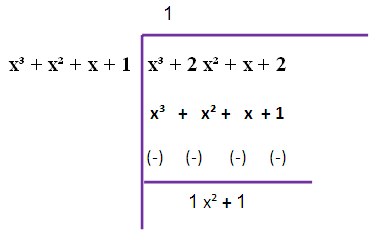
Since we are not getting zero, we have to do this long division once again

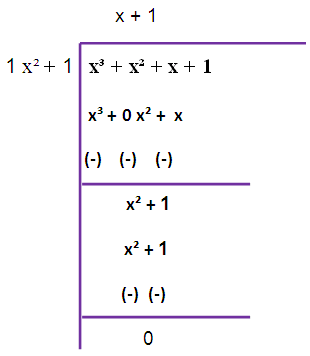
So, the required GCD is 2 (x²+1).

(iv) Answer :

x³-3x²+4x-12, x⁴+x³+4x²+4x

Let f(x) = x³-3x²+4x-12 and g(x) = x⁴+x³+4x²+4x

f(x) = x³-3x²+4x-12

g (x) = x(x³+x²+4x+4)

Here, deg (f(x)) = deg (g(x))

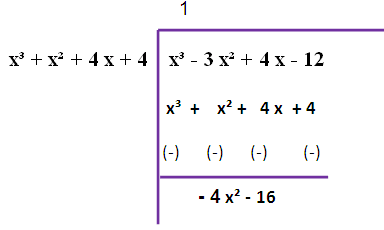
Since we are not getting zero, we have to do this long division once again

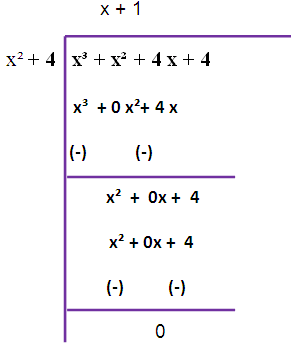
So, the required GCD is (x²+4).

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

About Us | Contact Us | Privacy Policy

USE THE EUCLIDEAN ALGORITHM TO FIND GCD OF THE GIVEN POLYNOMIALS

Recent Articles

US Common Core K-12 Curricum Algebra Solving Simple Equations

10 Hard SAT Math Questions (Part - 4)

10 Hard SAT Math Questions (Part - 3)