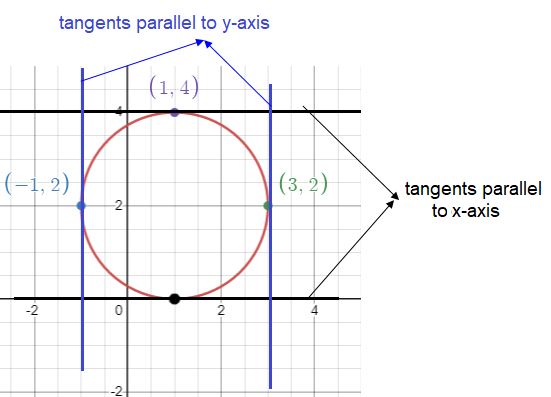
FIND THE POINTS ON THE CURVE WHERE THE TANGENT IS PARALLEL TO THE LINE
Example 1 :
Find at what points on a circle
x2 + y2 = 13
the tangent is parallel to the line 2x + 3y = 7.
Solution :
Since the tangent line drawn at the point to the circle is parallel to the given line, their slopes will be equal.
Slope of the given line 2x + 3y = 7.
m = -coefficient of x/coefficient of y
m = -2/3 ----(1)
We can find slope of the tangent by finding the derivation.
2x + 2y(dy/dx) = 0
2y(dy/dx) = -2x
dy/dx = -x/y ----(2)
(1) = (2)
-2/3 = -x/y
2y = 3x
y = 3x/2
By applying the value of y in the equation of circle, we get
x2 + y2 = 13
x2 + (3x/2)2 = 13
x2 + (9x2/4) = 13
13x2/4 = 13
x2 = 13(4/13)
x2 = 4
x = ± 2
|
If x = 2, then y = 3 |
If x = -2, then y = -3 |
So, the required points are (2, 3) (-2, -3).
Example 2 :
At what points on the curve
x2 + y2 - 2x - 4y + 1 = 0
the tangent is parallel to
(i) x - axis (ii) y - axis
Solution :
Since the tangent line drawn at the point is parallel to x - axis, slope of line will be equal to 0.
2x + 2y(dy/dx) - 2 - 4(dy/dx) = 0
2x + 2y(dy/dx) - 2 - 4(dy/dx) = 0
2y(dy/dx) - 4(dy/dx) = -2x + 2
(dy/dx)(2y - 4) = 2(-x + 1)
dy/dx = (-x + 1)/(y - 2)
If dy/dx =0
(-x + 1)/(y - 2) = 0
-x + 1 = 0
x = 1
By substituting the value of x = 1, in the given curve, we may solve for y.
x2 + y2 - 2x - 4y + 1 = 0
12 + y2 - 2 - 4y + 1 = 0
y2 - 4y = 0
y(y - 4) = 0
y = 0 and y = 4
So, the required points are (1, 0) and (1, 4).
(ii) y - axis
Solution :
When the tangent line is parallel to y-axis, the slope will become undefined. So, we may consider dy/dx = ∞ or 1/0
m (or) (dy/dx) = 1/0
dy/dx = (-x + 1)/(y - 2)
(-x + 1)/(y - 2) = 1/0
Doing cross multiplication, we get
0 = y - 2
y = 2
By substituting the value of y in the given equation, we may solve for x.
x2 + 22 - 2x - 4(2) + 1 = 0
x2 + 4 - 2x - 8 + 1 = 0
x2 - 2x - 3 = 0
(x - 3)(x + 1) = 0
x = 3 and x = -1
So, the required points are (3, 2) (-1, 2).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Sum and Difference Identities
May 07, 24 09:17 AM
Trigonometry Sum and Difference Identities - Concept - Solved Problems -
Trigonometry Even and Odd Iidentities
May 05, 24 12:25 AM
Trigonometry Even and Odd Iidentities -
SOHCAHTOA Worksheet
May 03, 24 08:50 PM
SOHCAHTOA Worksheet