SOHCAHTOA WORKSHEET

Problems 1-2 : For all the six trigonometric ratios of angle θ.

Problem 1 :

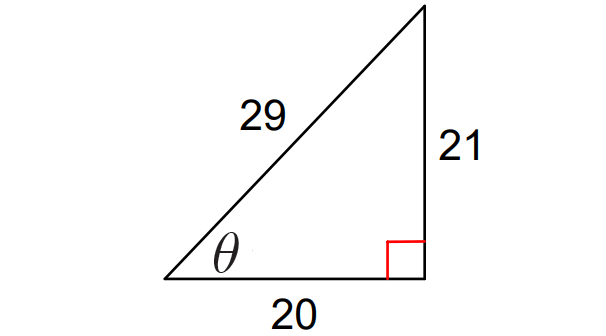
Problem 2 :

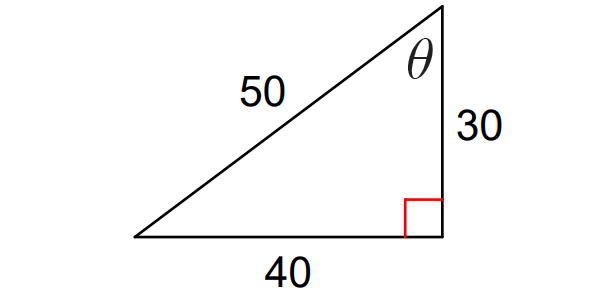
Problem 3 :

Find the value of of sin C in the ΔABC shown below.

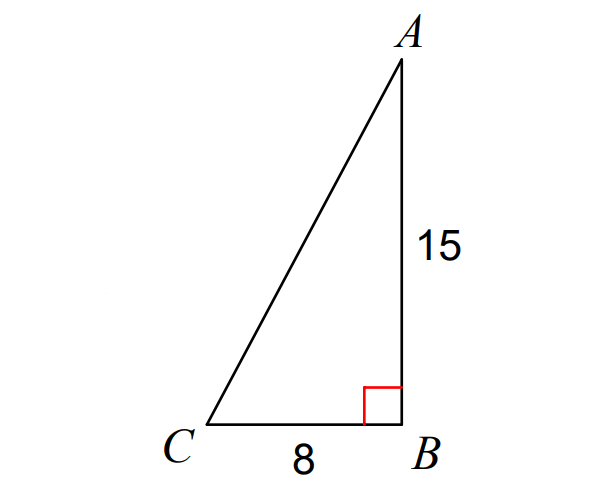
Problem 4 :

Find the value of of cos A in the ΔABC shown below.

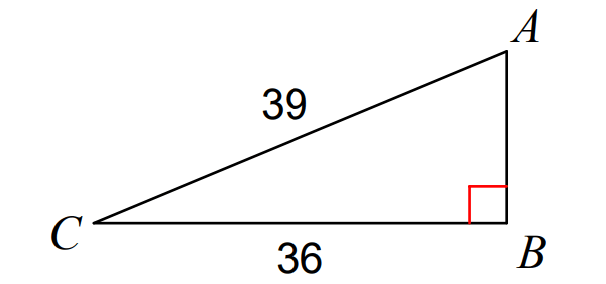
Problem 5 :

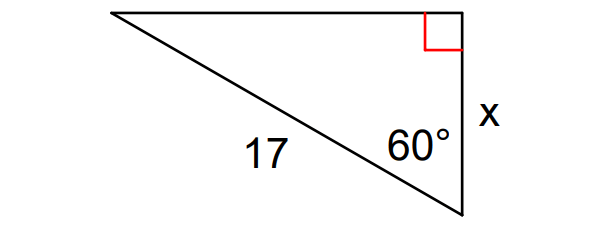
Find the value of x in the triangle shown below. Round to the nearest tenth.

Problem 6 :

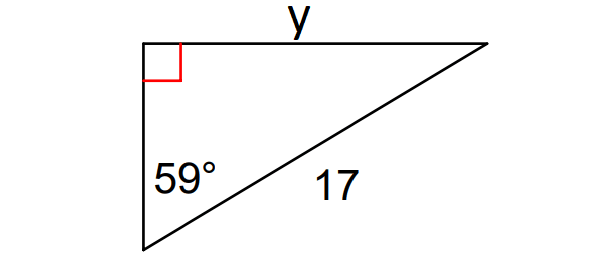
Find the value of y in the triangle shown below. Round to the nearest tenth.

Problem 7 :

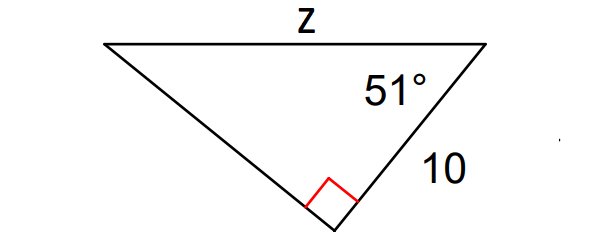
Find the value of z in the triangle shown below. Round to the nearest tenth.

Problems 8-10 : Find the value of x in the given triangle. Round to the nearest degree.

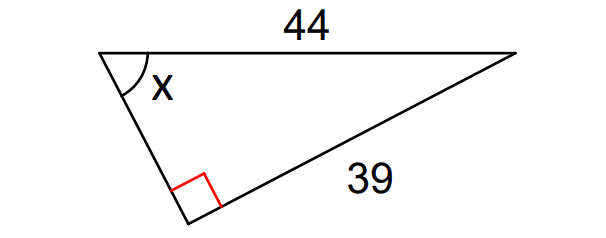
Problem 8 :

Problem 9 :

Problem 10 :

Problem 11 :

Find the angle made by a ladder of length 5m with the ground, if one of its end is 4m away from the wall and the other end is on the wall. (Round your answer to the nearest degree)

Problem 12 :

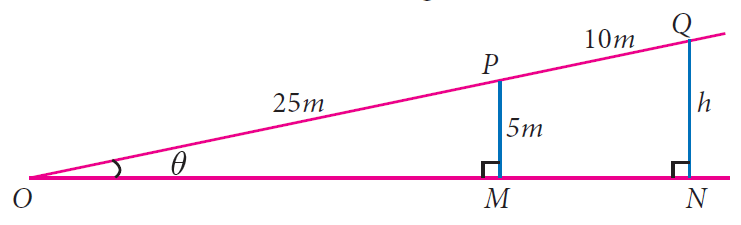
A boy standing at a point O finds his kite flying at a point P with distance OP = 25m. It is at a height of 5m from the ground. When the thread is extended by 10m from P, it reaches a point Q. What will be the height QN of the kite from the ground? (use trigonometric ratios)

Answers

1. Answer :

Considering angle θ in the triangle shown above,

opposite side = 21

adjacent side = 20

hypotenuse = 29

sin θ = ᵒᵖᵖ⁄hyp = ²¹⁄₂₉

cos θ = ᵃᵈʲ⁄hyp = ²⁰⁄₂₉

tan θ = ᵒᵖᵖ⁄ₐdⱼ = ²¹⁄₂₀

csc θ = ʰʸᵖ⁄ₒpp = ²⁹⁄₂₁

sec θ = ʰʸᵖ⁄ₐdⱼ = ²⁹⁄₂₀

cot θ = ᵃᵈʲ⁄ₒpp = ²⁰⁄₂₁

2. Answer :

Considering angle θ in the triangle above,

opposite side = 40

adjacent side = 30

hypotenuse = 50

sin θ = ᵒᵖᵖ⁄hyp = ⁴⁰⁄₅₀ = ⅘

cos θ = ᵃᵈʲ⁄hyp = ³⁰⁄₅₀ = ⅗

tan θ = ᵒᵖᵖ⁄ₐdⱼ = ⁴⁰⁄₃₀ = ⁴⁄₃

csc θ = ʰʸᵖ⁄ₒpp = ⁵⁰⁄₄₀ = ⁵⁄₄

sec θ = ʰʸᵖ⁄ₐdⱼ = ⁵⁰⁄₃₀ = ⁵⁄₃

cot θ = ᵃᵈʲ⁄ₒpp = ³⁰⁄₄₀ = ¾

3. Answer :

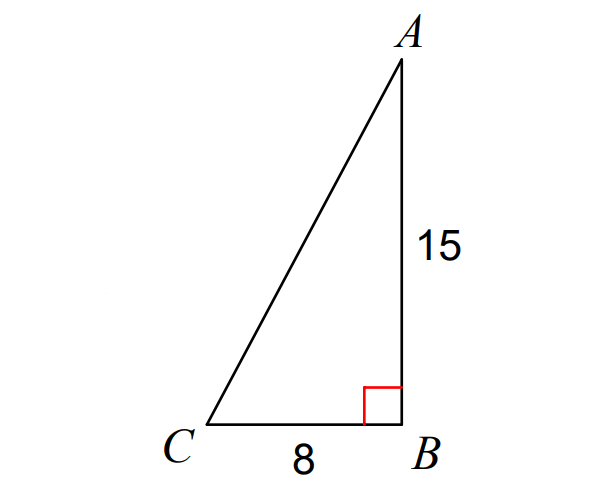
Using Pythagorean Theorem in the triangle above,

AC² = AB² + BC²

AC² = 15² + 8²

AC² = 225 + 64

AC² = 289

AC² = 17²

AC = 17

In ΔABC above, AC is hypotenuse. Considering angle C, AB is opposite side.

sin C = ᵒᵖᵖ⁄hyp

= ¹⁵⁄₁₇

4. Answer :

Using Pythagorean Theorem in the triangle above,

AC² = AB² + BC²

39² = AB² + 36²

1521 = AB² + 1296

225 = AB²

15² = AB²

15 = AB

In ΔABC above, AC is hypotenuse. Considering angle A, AB is adjacent side.

cos A = ᵃᵈʲ⁄hyp

= ¹⁵⁄₃₉

5. Answer :

In the triangle above, considering angle 60°,

adjacent side = x

hypotenuse = 17

So, we have to use the trigonometric ratio cosine to find the value of x.

cos 60° = ᵃᵈʲ⁄hyp

cos 60° = ˣ⁄₁₇

Multiply both sides by 17.

17(cos 60°) = x

Using calculator,

17(0.5) = x

x = 8.5

6. Answer :

In the triangle above, considering angle 59°,

opposite side = y

hypotenuse = 17

So, we have to use the trigonometric ratio sine to find the value of x.

sin 59° = ᵒᵖᵖ⁄hyp

sin 59° = ʸ⁄₁₇

Multiply both sides by 17.

17(sin 59°) = x

Using calculator,

17(0.8571.....) = x

x ≈ 14.6

7. Answer :

In the triangle above, considering angle 51°,

adjacent side = 10

hypotenuse = z

So, we have to use the trigonometric ratio cosine to find the value of z.

cos 51° = ᵃᵈʲ⁄hyp

cos 51° = ¹⁰⁄z

0.6293..... = ¹⁰⁄z

Take reciprocal on both sides.

¹⁄₀.₆₂₉₃..... = ᶻ⁄₁₀

Multiply both sides by 10.

15.9 ≈ z

8. Answer :

In the triangle above, considering angle x,

opposite side = 39

hypotenuse = 44

So, we have to use the trigonometric ratio sine to find the value of x.

sin x = ᵒᵖᵖ⁄hyp

sinx = ³⁹⁄₄₄

x = sin^-1(³⁹⁄₄₄)

x = sin^-1(0.8863......)

x ≈ 62°

9. Answer :

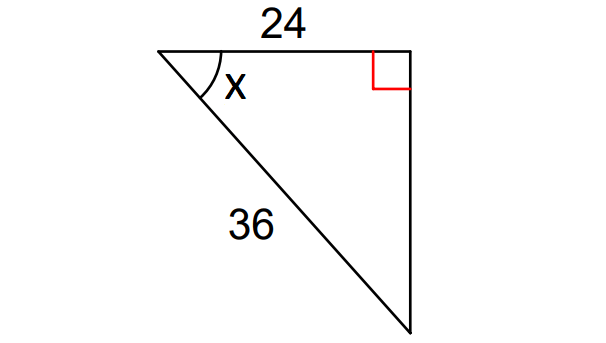
In the triangle above, considering angle x,

adjacent side = 24

hypotenuse = 36

So, we have to use the trigonometric ratio cosine to find the value of x.

cos x = ²⁴⁄₃₆

cos x = ⅔

x = cos^-1(⅔)

x = cos^-1(0.6666......)

x ≈ 48°

10. Answer :

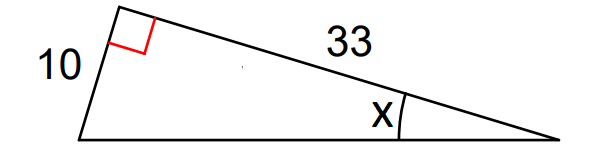
In the triangle above, considering angle x,

opposite side = 10

adjacent side = 33

So, we have to use the trigonometric ratio tangent to find the value of x.

tan x = ¹⁰⁄₃₃

x = tan^-1(¹⁰⁄₃₃)

x = tan^-1(0.3030......)

x ≈ 17°

11. Answer :

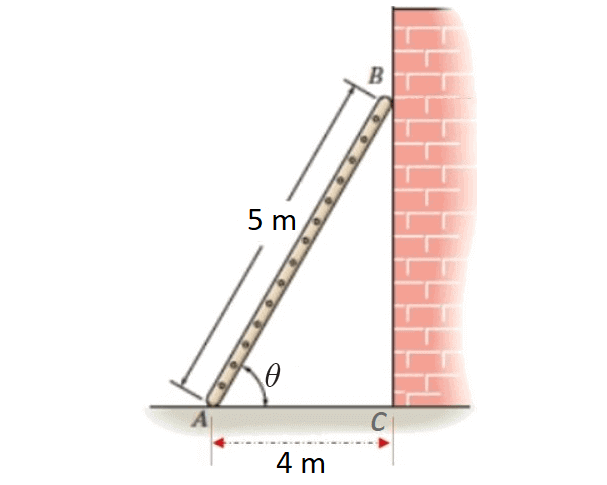
In ΔABC above, considering angle θ,

adjacent side = AC = 4

hypotenuse = AB = 5

So, we have to use the trigonometric ratio cosine to find the angle θ.

cos θ = ⅘

θ = cos^-1(⅘)

θ = cos^-1(0.8)

θ ≈ 37°

The angle made by the ladder with the ground is about 37°.

12. Answer :

In ΔOPM and ΔOQN,

m∠O ≅ m∠O (Reflexive Property)

m∠M ≅ m∠Q (Right Angles)

Two angles of ΔOPM are congruent to two angles of ΔOQN.

By Angle-Angle Similarity Postulate, ΔOPM and ΔOQN are similar triangles.

Find the value of sin θ in ΔOPM.

sin θ = ⁵⁄₂₅

sin θ = ⅕

Find the value of sin θ in ΔOQN.

sin θ = ʰ⁄₃₅

Since ΔOPM and ΔOQN are similar triangles, the values of sin θ in ΔOPM and ΔOQN must be equal.

ʰ⁄₃₅ = ⅕

Multiply both sides by 35.

h = 7

The height QN of the kite from the ground will be 7m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.