TRIGONOMETRY - Even and Odd Iidentities

Let f(x) be a function.

In general, to find whether f(x) is an even or odd function, we will plugin -x for x into f(x) and do the following check. 

f(-x) = f(x) ----> f(x) is even function

f(-x) = -f(x) ----> f(x) is odd function

In trigonometry, we have the following six ratios

sin θ

csc θ

cos θ

sec θ

tan θ

cot θ

To find each of the above trigonometric ratios is even or odd, we have replace θ by -θ.

For example, in sin θ, if we replace θ by -θ, it becomes

sin (-θ)

In sin (-θ), the angle is negative. In a trigonometric ratio, if the angle is negative, we will consider quadrant IV.

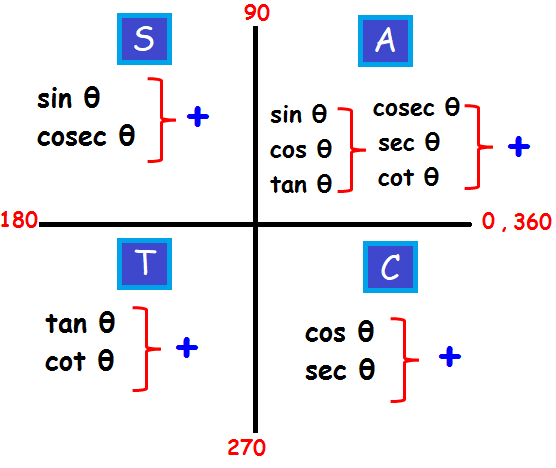
In quadrant IV, the trigonometric ratios cosine and secant are positive and the remaning four trigonometric ratios are negative.

Then, we have

cos (-θ) = cos θ

sec (-θ) = sec θ

sin (-θ) = -sin θ

csc (-θ) = -csc θ

tan (-θ) = -tan θ

cot (-θ) = -cot θ

Since

cos (-θ) = cos θ

sec (-θ) = sec θ,

cos θ and sec θ are even trigonometric ratios and the rest are odd trigonometric ratios.

Solved Problems

Problem 1 :

If the value of cos θ = 0.5, fins the value of cos (-θ).

Solution :

Since cos θ is even, we have

cos (-θ) = cos θ

= 0.5

Problem 2 :

If the value of tan θ = 1.2, find the value of tan (-θ).

Solution :

Since tan θ is odd, we have

tan (-θ) = -tan θ

= -1.2

Problem 3 :

If the value of csc θ = -2, find the value of csc (-θ).

Solution :

Since csc θ is odd, we have

csc (-θ) = -csc θ

= -(-2)

= 2

Problem 4 :

Solution :

Since cos θ is even, we have

Since tan θ is odd, we have

Evaluating sin θ :

Problem 5 :

Solution :

Since cos θ is even, we have

Since sin θ is odd, we have

Evaluating tan θ :

Problem 6 :

If the value of cos 60° = 0.5, find the value of cos (-480°).

Solution :

Since cos θ is even, we have

cos (-480°) = cos 480°

= cos (360° + 120°)

= cos 120°

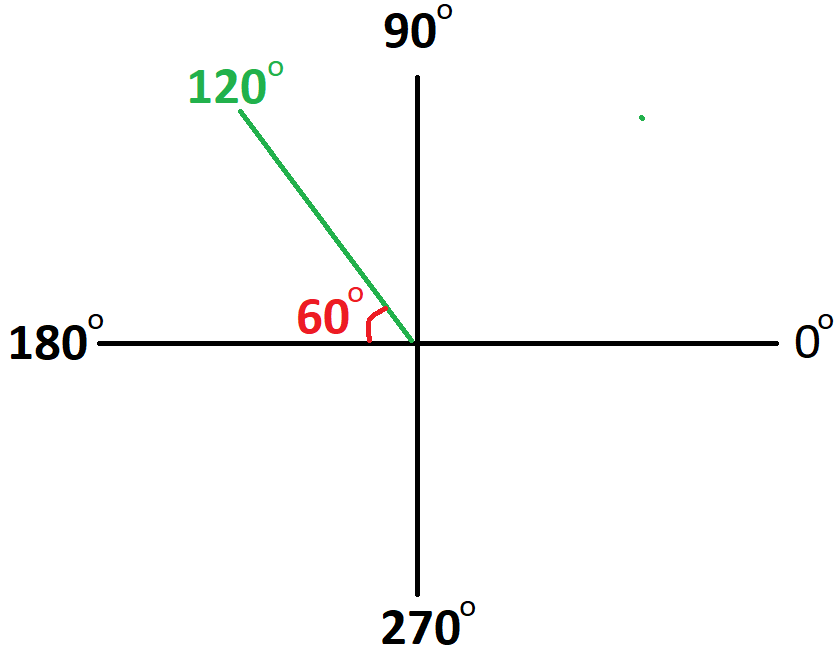
120° is in quadrant II and its reference angle is 60°.

And also, cosine is negative in quadrant II.

= -cos 60°

= -0.5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.