TRIGONOMETRY - Sum and Difference Identities

Solved Problems

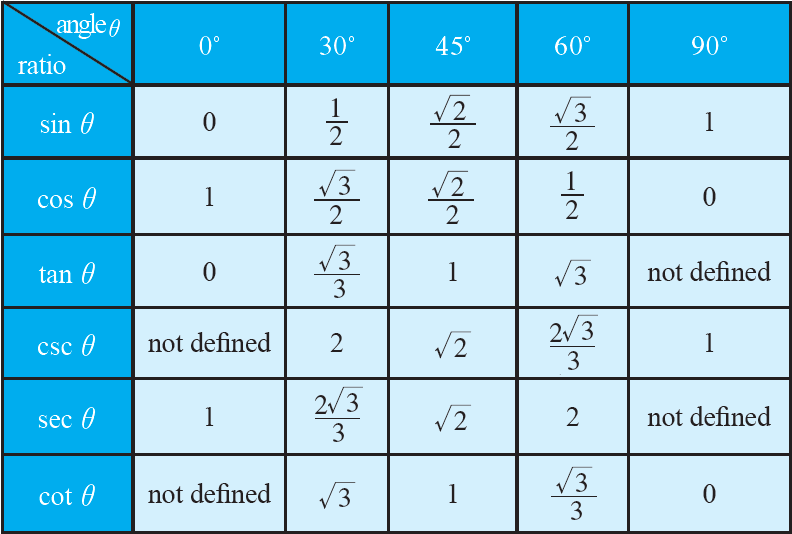
Problems 1-4 : Use the trigonometric ratio table given below to evaluate the given trigonometric ratio.

Problem 1 :

cos 15°

Solution :

= cos 15°

= cos (45° - 30°)

Use the identity of cos (A - B).

= cos 45° cos 30° + sin 45° sin 30°

Substitute the values for the trigonometric ratios from the table above.

Problem 2 :

cos 105°

Solution :

= cos 105°

= cos (60° + 45°)

Use the identity of cos (A + B).

= cos 60° cos 45° - sin 60° sin 45°

Substitute the values for the trigonometric ratios from the table above.

Problem 3 :

sin 75°

Solution :

= sin 75°

= sin (45° + 30°)

Use the identity of sin (A + B).

= sin 45° cos 30° + cos 45° sin 30°

Substitute the values for the trigonometric ratios from the table above.

Problem 4 :

tan 15°

Solution :

= tan 15°

= tan (45° - 30°)

Use the identity of tan (A - B).

Problem 5 :

If A and B are acute angles, find cos (A + B).

Solution :

Since A and B are acute angles, they lie in I^st quadrant. In I^st quadrant, all trigonometric ratios are psitive.

So,

Evaluating cos (A + B) :

= cos (A + B)

= cos A cos B - sin A sin B

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.