SURFACE AREA OF CUBE AND CUBOID WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Find the total surface area and lateral surface area of a cuboid whose length is 20 cm, width is 15 cm and height is 8 cm.
Problem 2 :
The dimensions of a cuboidal box are 6 m x 400 cm x 1.5 m. Find the cost of painting its entire outer surface at the rate of $22 per square meter.
Problem 3 :
The dimensions of a hall is 10 m x 9 m x 8 m. Find the cost of white washing the walls and ceiling at the rate of $8.50 per square meter.
Problem 4 :
The length, width and depth of a pond are 20.5 m, 16 m and 8 m respectively. Find the capacity of the pond in liters.
Problem 5 :
The outsides of purple traps are coated with glue to catch emerald ash borers. You make your own trap in the shape of a rectangular prism with an open top and bottom. What is the surface area that you need to coat with glue?
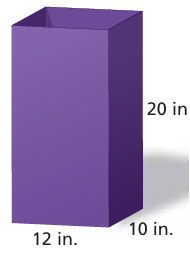
Problem 6 :
Which prism has the greater surface area?
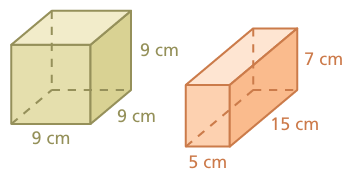
Problem 7 :
A public library has an aquarium in the shape of a rectangular prism. The base is 6 feet by 2.5 feet. The height is 4 feet. How many square feet of glass were used to build the aquarium? (The top of the aquarium is open.)

Problem 8 :
A label that wraps around a box of golf balls covers 75% of its lateral surface area. What is the value of x?

Problem 9 :
Write a formula for the surface area of a rectangular prism using the height h, the perimeter P of a base, and the area B of a base.
Answer Key
1) 560 cm2
2) $1716
3) $3349
4) 2624000 liters
5) 2624000 liters
6) 486 cm square
7) To make a aquarium, we need 60 square feet of glass.
8) the required length of the box is 4 feet.
9) total surface area of rectangular prism = 2B + Ph
Problem 1 :
Find the total surface area and lateral surface area of the cube whose side is
(i) 8 m (ii) 21 cm (iii) 7.5 cm
Problem 2 :
If the total surface area of a cube is 2400 cm2 then, find its lateral surface area.
Problem 3 :
A cubical container of side 6.5 m is to be painted on the entire outer surface. Find the area to be painted and the total cost of painting it at the rate of $24 per m2.
Problem 4 :
Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid.
Problem 5 :
A cubical tank can hold 64,000 liters of water. Find the length of its side in meters.
Problem 6 :
The side of a metallic cube is 12 cm. It is melted and formed into a cuboid whose length and width are 18 cm and 16 cm respectively. Find the height of the cuboid.
Problem 7 :
One can of frosting covers about 280 square inches. Is one can of frosting enough to frost the cake? Explain.
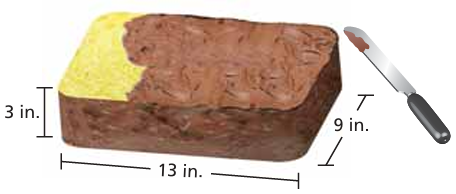
Problem 8 :
Fifty percent of the surface area of the bread is crust. What is the height h?

Problem 9 :
Compare the dimensions of the prism. How many times greater is the surface area of the red prism than the surface area of the blue prism?
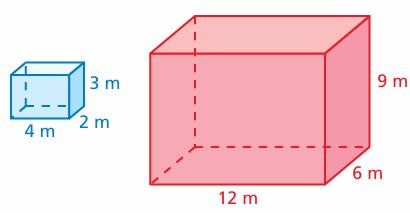
Problem 10 :
A keychain-sized puzzle cube is made up of small cubes. Each small cube has a surface area of 1.5 square inches.

a. What is the side length of each small cube?
b. What is the surface area of the entire puzzle cube?
Answer Key
1)
i) Total surface area = 384 m2
Lateral surface area = 256 m2
ii) Total surface area = 2646 cm2
Lateral surface area = 1764cm2
iii) Total surface area = 337.5 cm2
Lateral surface area = 225 cm2
2) 1600 cm2
3) $6084
4) Total surface area = 224 cm2
Lateral surface area = 128 cm2
5) length of the side of the tank is 4 meters.
6) h = 6 cm
7) one can of frosting cannot cover the cake.
8) the required height is 5 cm.
9) surface area of red prism is 9 times surface area of blue prism.
10) a) side lenght of the cube is 0.5 inch.
b) 13.5 square inches.
Problem 1 :
Erin is making a jewelry box of wood in the shape of a rectangular prism. The jewelry box will have the dimensions shown below. She plans to spray paint the exterior of the box. How many square inches will she have to paint ?
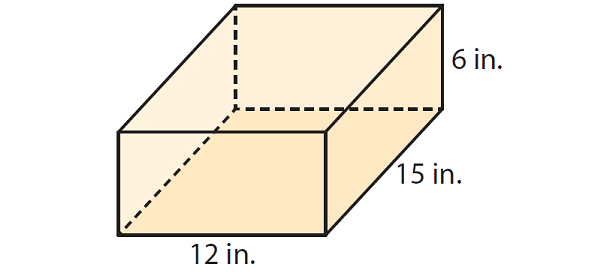
Problem 2 :
A brand of uncooked spaghetti comes in a box that is a rectangular prism with a length of 9 inches, a width of 2 inches, and a height of 1 1/2 inches. What is the surface area of the box ?
Problem 3 :
You are painting the prize pedestals shown (including the bottoms). You need 0.5 pint of paint to paint the red pedestal.
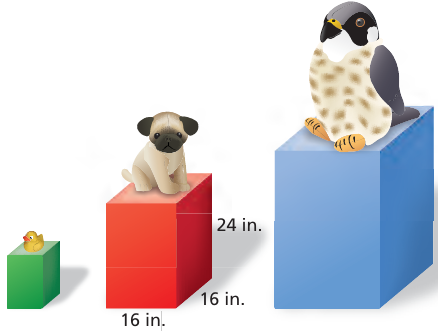
a. The side lengths of the green pedestal are one-half the side lengths of the red pedestal. How much paint do you need to paint the green pedestal?
b. The side lengths of the blue pedestal are triple the side lengths of the green pedestal. How much paint do you need to paint the blue pedestal?
c. Compare the ratio of paint amounts to the ratio of side lengths for the green and red pedestals. Repeat for the green and blue pedestals. What do you notice?
Problem 4 :
Compare the dimensions of the prisms. How many times greater is the surface area of the red prism than the surface area of the blue prism?
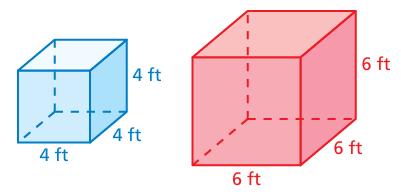
Answer Key
1) Erin will have to spray paint 684 square inches of wood.
2) the surface area of the box is 69 square inches.
3) a) 0.125 pints b) 1.125 pints
4) Ratio between green and red pedestals is 1 : 4
Ratio between green and blue pedestals is 1 : 9
5) surface area of red prism is 2.25 times surface area of blue prism.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
