FINDING THE SURFACE AREA OF A PRISM

When dimensions of a prism are given, we can use the appropriate formula to find surface area of the prism.

The formula given below can be used to find surface area of a prism.  

The surface area S of a prism with base perimeter P, height h and base area B is 

S  =  Ph + 2B

Example 1 : 

Erin is making a jewelry box of wood in the shape of a rectangular prism. The jewelry box will have the dimensions shown below. She plans to spray paint the exterior of the box. How many square inches will she have to paint ?

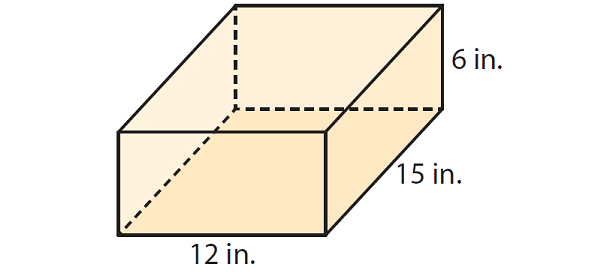
Solution : 

Step 1 :

Identify a base, and find its area and perimeter.

Any pair of opposite faces can be the bases. For example, we can choose the bottom and top of the box as the bases.

Find base area. 

B  =  l x w

B  =  12 x 15

B  =  180 square in.

Find perimeter of the base. 

P  =  2(12) + 2(15)

P  =  24 + 30

P  =  54 in.

Step 2 : 

Identify the height, and find the surface area.

The height h of the prism is 6 inches. Use the formula to find the surface area.

S  =  Ph + 2B

S  =  54(6) + 2(180)

S  =  684 square inches

So, Erin will have to spray paint 684 square inches of wood.

Example 2 : 

A brand of uncooked spaghetti comes in a box that is a rectangular prism with a length of 9 inches, a width of 2 inches, and a height of 1 1/2 inches. What is the surface area of the box ?

Solution : 

Step 1 :

Identify a base, and find its area and perimeter.

Any pair of opposite faces can be the bases. For example, we can choose the bottom and top of the box as the bases.

Find base area. 

B  =  l x w

B  =  9 x 2

B  =  18 square in.

Find perimeter of the base. 

P  =  2(9) + 2(2)

P  =  18 + 4

P  =  22 in.

Step 2 : 

Identify the height, and find the surface area.

The height h of the prism is 1 1/2 inches. Use the formula to find the surface area.

S  =  Ph + 2B

S  =  22(1 1/2) + 2(18)

S  =  22(3/2) + 36

S  =  33 + 36

S  =  69 square inches

So, the surface area of  the box is 69 square inches. 

Example 3 : 

You are painting the prize pedestals shown (including the bottoms). You need 0.5 pint of paint to paint the red pedestal.

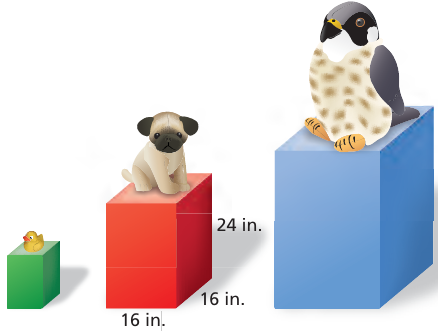
a. The side lengths of the green pedestal are one-half the side lengths of the red pedestal. How much paint do you need to paint the green pedestal?

b. The side lengths of the blue pedestal are triple the side lengths of the green pedestal. How much paint do you need to paint the blue pedestal?

c. Compare the ratio of paint amounts to the ratio of side lengths for the green and red pedestals. Repeat for the green and blue pedestals. What do you notice?

Solution :

Surface area of red pedestal = 2(lw + wh + hl)

Measures of red pedestal :

length = 16 in, width = 16 in  and height = 24 in

= 2(16⋅16 +16⋅24 + 24⋅16)

= 2(256 + 384 + 384)

= 2(1024)

= 2048 square inches

Amount of paint need to paint red pedestal = 0.5 pint

Amount of paint needed to 1 square inch = 0.5/2048

a) Measures of green pedestal :

One half lengths of red pedestal,

length = 8 in, width = 8 in  and height = 12 in

= 2(8⋅8 + 8⋅12 + 12⋅8)

= 2(64 + 96 + 96)

= 2(256)

= 512 square inches

Amount of paint needed to paint green pedestal

= 512(0.5/2048)

= 0.125 pints

b) Measures of blue pedestal :

Triple the lengths of green pedestal,

length = 24 in, width = 24 in  and height = 36 in

= 2(24⋅24 + 24⋅36 + 36⋅24)

= 2(576 + 864 + 864)

= 2(2304)

= 4608 square inches

Amount of paint needed to paint blue pedestal

= 4608(0.5/2048)

= 1.125 pints

c) Ratio between green and red pedestals

= 512/2048

= 1/4

= 1 : 4

Ratio between green and blue pedestals = 512/4608

= 1/9

= 1 : 9

Example 4 : 

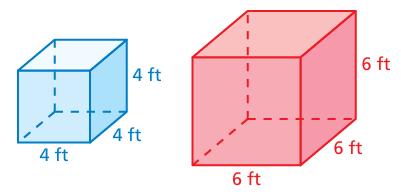
Compare the dimensions of the prisms. How many times greater is the surface area of the red prism than the surface area of the blue prism?

Solution :

Dimensions of blue prism :

length = 4 ft, width = 4 ft, height = 4ft

Surface area = 6a² 

= 6(4)²

= 6(16)

= 96 sq.ft

Dimensions of blue prism :

length = 6 ft, width = 6 ft, height = 6 ft

Surface area = 6a² 

= 6(6)²

= 6(36)

= 216 sq.ft

Surface area of red prism = n (surface area of blue prism)

216 = n(96)

n = 216/96

n = 2.25

So, surface area of red prism is 2.25 times surface area of blue prism.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.