SOLVING MENSURATION WORD PROBLEMS WITH THE SHAPE CUBE

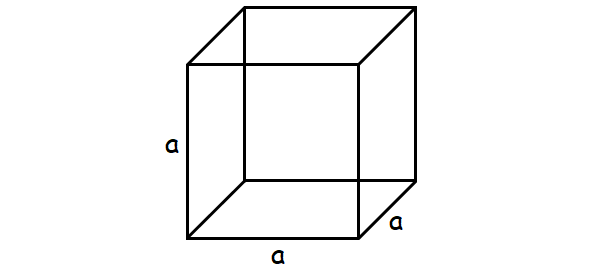
If the side of a cube is a units, then,

total surface area = 6a² square units

lateral surface area = 4a² square units

volume = a³ cubic units

Problem 1 :

Find the total surface area and lateral surface area of the cube whose side is

(i) 8 m (ii) 21 cm (iii) 7.5 cm

Solution :

(i) Side length is 8 m :

Total surface area = 6a²

= 6(8)²

= 6(64)

= 384 m²

Lateral surface area = 4a²

= 4(8)²

= 4(64)

= 256 m²

(ii) Side length is 21 cm :

Total surface area = 6a²

= 6(21)²

= 6(441)

= 2646 cm²

Lateral surface area = 4a²

= 4(21)²

= 4(441)

= 1764cm²

(iii) Side length is 7.5 cm :

Total surface area = 6a²

= 6(7.5)²

= 6(56.25)

= 337.5 cm²

Lateral surface area = 4a²

= 4(7.5)²

= 4(56.25)

= 225 cm²

Problem 2 :

If the total surface area of a cube is 2400 cm² then, find its lateral surface area.

Solution :

Total surface area = 2400 cm²

6a² = 2400

a² = 2400/6

a² = 400

a = 20 cm

Lateral surface area :

= 4a²

  = 4(20)²

  = 4(400)

  = 1600 cm²

Problem 3 :

A cubical container of side 6.5 m is to be painted on the entire outer surface. Find the area to be painted and the total cost of painting it at the rate of $24 per m².

Solution :

Side length of cubical container = 6.5 m

Total surface area of the container :

= 6a²

  = 6(6.5)²

  = 6(42.25)

  = 253.5 m²

Total cost of painting at the rate of $24 per m² :

= 253.5(24)

= $6084

Problem 4 :

Three identical cubes of side 4 cm are joined end to end. Find the total surface area and lateral surface area of the new resulting cuboid.

Solution :

Resulting cuboid :

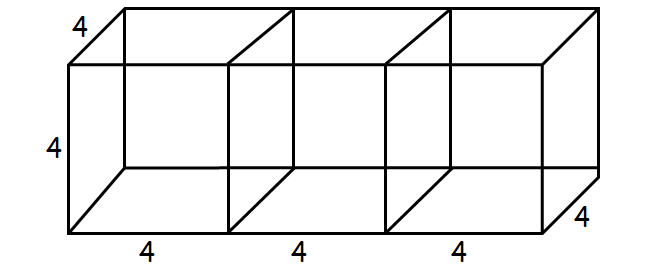
Length of resulting cuboid :

= 4 + 4 + 4

= 12 cm

Width = 4 cm and height = 4 cm

Total surface area of resulting cuboid : 

= 2(lb + bh + hl)

  = 2[12(4) + 4(4) + 4(12)]

= 2 [48 + 16 + 48]

= 2(112)

= 224 cm²

Lateral surface area of resulting cuboid :

= 2h(l + w)

= 2(4)(12 + 4)

= 2(4)(16)

= 128 cm²

Problem 5 :

A cubical tank can hold 64,000 liters of water. Find the length of its side in meters.

Solution :

Let ‘a’ be the side of cubical tank.

Volume = 64000 liters

1000 liters = 1 m³,

Volume = 64000/1000 m³

Volume = 64 m³

a³ = 64

a³ = 4³

a = 4

Therefore, length of the side of the tank is 4 meters.

Problem 6 :

The side of a metallic cube is 12 cm. It is melted and formed into a cuboid whose length and width are 18 cm and 16 cm respectively. Find the height of the cuboid.

Solution :

volume of cuboid = volume of cube

l x w x h = a³

18 x 16 x h = 12³

288h = 1728

Divide each side by 288.

h = 6 cm

Problem 7 :

One can of frosting covers about 280 square inches. Is one can of frosting enough to frost the cake? Explain.

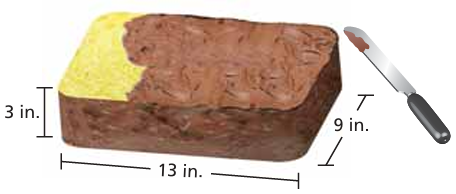
Solution :

Total surface area of covered by frosting 

= 2(lw + wh + hl)

length = 13 inches, width = 9 inches and heigth = 3 inches

= 2(13 ⋅ 9 + 9 ⋅ 3 + 3 ⋅13)

= 2(117 + 27 + 39)

= 2(183)

= 366 square inches

So, one can of frosting cannot cover the cake.

Problem 8 :

Fifty percent of the surface area of the bread is crust. What is the height h?

Solution :

length = 10 cm, width = 10 cm and height = h

Surface area of rectangular prism can be calculated in two different ways,

• Usign the formula 2(lw + wh + hl)
• Using the formula 2B + Ph
• Here B is the base area, h is height and P is perimeter of base. 

Quantity of crust = 50% of surface area of bread

Crust of the bread will be out layer of the bread.  

200 = 0.50[2(10⋅10) + 40h]

200 = 0.50[200 + 40h]

200/0.50 = 200 + 40h

400 = 200 + 40h

400 - 200 = 40h

40h = 200

h = 200/40

h = 5

So, the required height is 5 cm.

Problem 9 :

Compare the dimensions of the prism. How many times greater is the surface area of the red prism than the surface area of the blue prism?

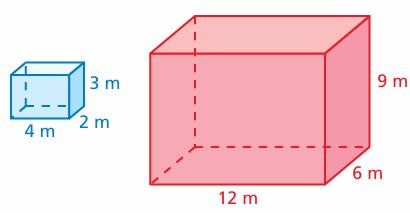
Solution :

Surface area of red prism = n(surface area of cube)

2(12(6) + 6(9) + 9(12)) = 2n[4(3) + 3(2) + 4(2)]

2[72 + 54 + 108] = 2n[12 + 6 + 8]

234 = n[26]

n = 234/26

n = 9

So, surface area of red prism is 9 times surface area of blue prism.

Problem 10 :

A keychain-sized puzzle cube is made up of small cubes. Each small cube has a surface area of 1.5 square inches.

a. What is the side length of each small cube?

b. What is the surface area of the entire puzzle cube?

Solution :

a) Surface area of small cube = 6s²

Here s is the side length

6s² = 1.5

s² = 1.5/6

s² = 0.25

s = 0.5

So, side lenght of the cube is 0.5 inch.

b) Number of small cubes in each side = 3

Side lenght of large cube = 3(0.5)

= 1.5

Surface area of entire puzzle = 6(1.5)²

= 6(2.25)

= 13.5 square inches.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.